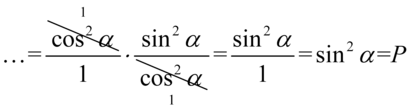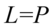Przykład 127
[kliknij aby rozwinąć] 
Założenie: 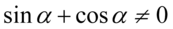 (mianownik nie może być równy
(mianownik nie może być równy  ). Po przekształceniu otrzymujemy
). Po przekształceniu otrzymujemy  .
.
Przestrzegam przed skracaniem w stylu 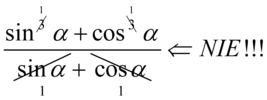 , ponieważ znak dodawania wraz z otaczającymi elementami musi być zamknięty w nawiasie. Po zamknięciu w nawiasie
, ponieważ znak dodawania wraz z otaczającymi elementami musi być zamknięty w nawiasie. Po zamknięciu w nawiasie 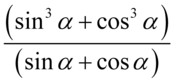 nie mamy już czego skrócić, ponieważ pojedynczych elementów z wnętrza nawiasu nie wolno skracać.
nie mamy już czego skrócić, ponieważ pojedynczych elementów z wnętrza nawiasu nie wolno skracać.
Zajmiemy się lewą stroną, ponieważ daje ona więcej możliwości przekształceń. Na początku trzeba zauważyć, że w liczniku mamy wzór skróconego mnożenia postaci 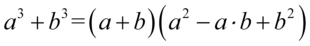 i w związku z tym musimy się zastanowić co podniesione do potęgi trzeciej daje
i w związku z tym musimy się zastanowić co podniesione do potęgi trzeciej daje 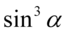 i
i 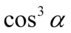 :
:
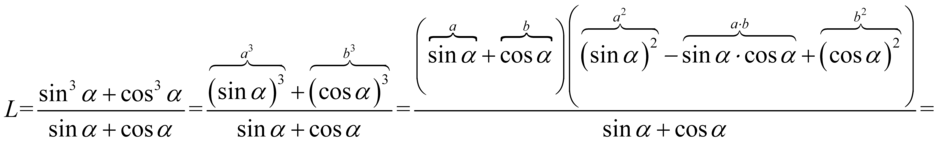
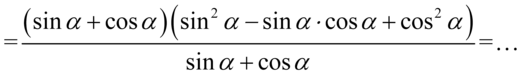
Na tym etapie możemy skrócić pierwszy nawias z licznika z całym mianownikiem:
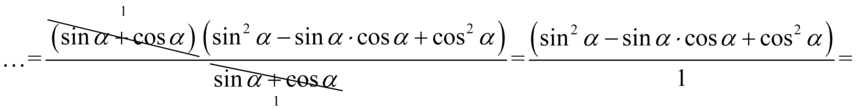
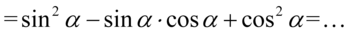
Teraz zmienimy nieco kolejność składników tzn. warto „przytulać” do siebie sinusy i cosinusy podniesione do kwadratu, ponieważ dzięki temu uzyskujemy jedynkę trygonometryczną:
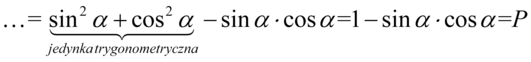
Przykład 128
[kliknij aby rozwinąć] 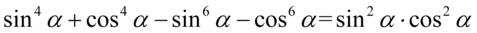
Lewa strona tożsamości jest dłuższa i występują tu większe potęgi, zatem to ona będzie podlegać przekształceniom. Trzeba się tu wykazać pomysłowością. W celu „zbicia” potęg do niższych wartości najpierw zmienimy kolejność składników tak, aby sinusy sąsiadowały ze sobą – podobnie cosinusy. Oczywiście nie zmieni to wartości wyrażenia:
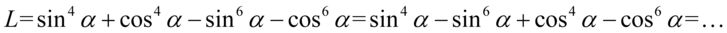
Teraz pogrupujemy w nawiasy po dwa składniki i to też nie zmieni wartości przekształcanego wyrażenia:

Kolejny krok to wyciągnięcie z każdego nawiasu możliwie największego wspólnego czynnika (czyli elementu powtarzającego się). Pamiętamy, że jeśli przy wykonywaniu tej operacji wyciągamy wszystko to zostaje  :
:

Z powstałego wyrażenia znów wyciągniemy możliwie największy czynnik:
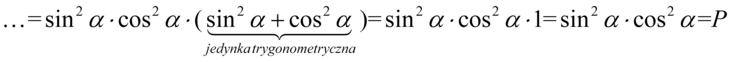
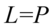
Przykład 129
[kliknij aby rozwinąć] 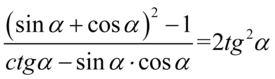
Założenie: 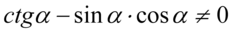 (mianownik ułamka nigdy nie może być równy
(mianownik ułamka nigdy nie może być równy  ). Po przeniesieniu jednego składnika założenia otrzymujemy
). Po przeniesieniu jednego składnika założenia otrzymujemy  .
.
Ostrzegam przed skracaniem w stylu 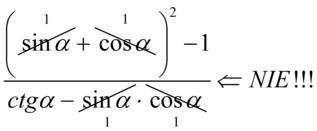 . Pojedynczych elementów z wnętrza nawiasu nie wolno skracać. Skraca się cały nawias lub wcale.
. Pojedynczych elementów z wnętrza nawiasu nie wolno skracać. Skraca się cały nawias lub wcale.
Lewa strona równości jest dłuższa, zatem to ona będzie podlegać przekształceniom. Na początku pozbędziemy się nawiasu z licznika korzystając ze wzoru skróconego mnożenia 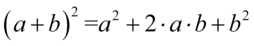 :
:
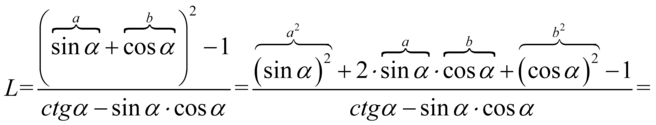
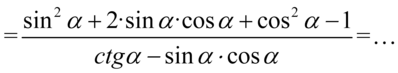
Przyjrzyjmy się licznikowi, występuje tu 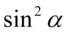 oraz
oraz 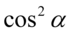 , które warto do siebie „przytulać”, ponieważ dodane do siebie stworzą jedynkę trygonometryczną. W tym celu zmienimy nieco kolejność składników, co i tak nie zmieni wartości wyrażenia:
, które warto do siebie „przytulać”, ponieważ dodane do siebie stworzą jedynkę trygonometryczną. W tym celu zmienimy nieco kolejność składników, co i tak nie zmieni wartości wyrażenia:
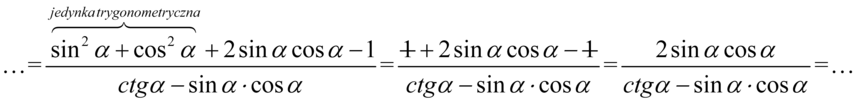
Na razie zostawimy licznik, bo właściwie nie można nic tu zrobić i zajmijmy się mianownikiem. Jedyną sensowną i możliwą operacją jest tu pozbycie się cotangensa korzystając z formuły 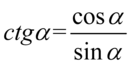 :
:
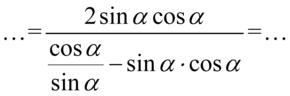
Teraz dolne piętro „megaułamka” postaramy się zapisać za pomocą jednego wyrażenia - czyli na jednej kresce ułamkowej. Dla ułatwienia działań zastosujemy zapis 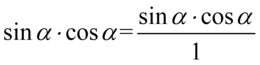 :
:
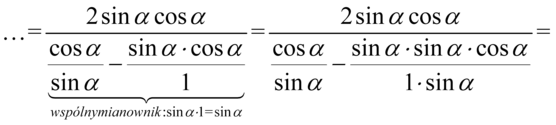

W celu maksymalnego uproszczenia powstałego ułamka wyciągnijmy powtarzający się element tzn. 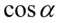 jako wspólny czynnik przed nawias. Pamiętamy, że zabierając wszystko przy wyciąganiu zostaje
jako wspólny czynnik przed nawias. Pamiętamy, że zabierając wszystko przy wyciąganiu zostaje 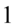 :
:
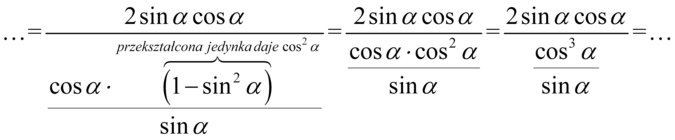
Teraz pozbędziemy się piętrowego ułamka zastępując główną kreskę ułamkową znakiem dzielenia, a następnie zamieniając dzielenie na mnożenie przez odwrotność:
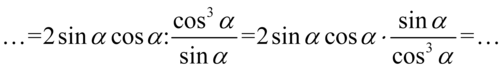
Dla ułatwienia skracania zastosujemy zapis 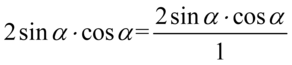 oraz ponownie rozpiszemy
oraz ponownie rozpiszemy 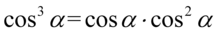 :
:
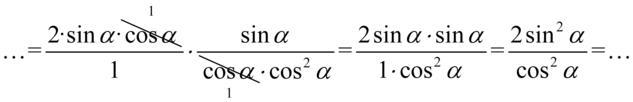
Aby otrzymać prawą stronę tożsamości musimy uzyskać jeszcze 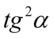 . W związku z tym najpierw skorzystamy z własności potęg
. W związku z tym najpierw skorzystamy z własności potęg 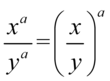 (w naszym przypadku
(w naszym przypadku 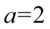 ):
):
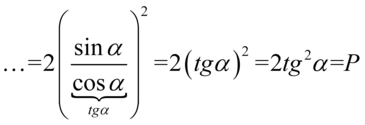
Przykład 130
[kliknij aby rozwinąć] 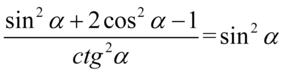
Założenie: 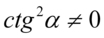 (mianownik nie może być równy
(mianownik nie może być równy  ). Po przekształceniu założenia otrzymujemy
). Po przekształceniu założenia otrzymujemy 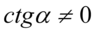 , ponieważ cotangens podniesiony do kwadratu jest różny od zera tylko wtedy gdy sam cotangens jest różny od zera.
, ponieważ cotangens podniesiony do kwadratu jest różny od zera tylko wtedy gdy sam cotangens jest różny od zera.
Lewa strona tożsamości jest dłuższa, zatem to ona będzie przekształcana. Na początku zmodyfikujemy nieco licznik, ponieważ występują w nim 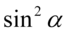 i
i 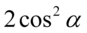 , które można zamienić na jedynkę trygonometryczną, przeszkadza nam tylko
, które można zamienić na jedynkę trygonometryczną, przeszkadza nam tylko 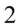 . Nie stanowi to jednak problemu, bo
. Nie stanowi to jednak problemu, bo 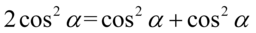 :
:
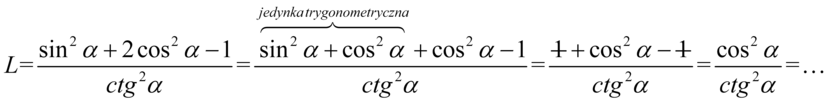
Kolejny krok stanowi zlikwidowanie cotangensa zgodnie ze wzorem 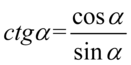 , ponieważ po prawej stronie tożsamości cotangens nie występuje:
, ponieważ po prawej stronie tożsamości cotangens nie występuje:
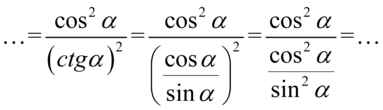
Na zakończenie zastąpimy główną kreskę ułamkową znakiem dzielenia, a następnie zamienimy dzielenie na mnożenie przed odwrotność drugiego składnika:
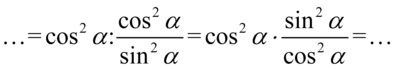
Aby było wiadomo, jak skracać ułamki zastosujemy zapis 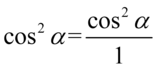 , ponieważ każda liczba lub wyrażenie podzielone przez
, ponieważ każda liczba lub wyrażenie podzielone przez  nie ulega zmianie:
nie ulega zmianie: