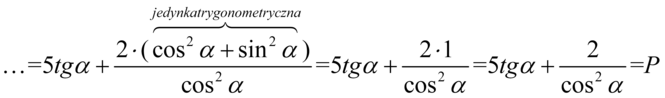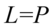Przykład 123
[kliknij aby rozwinąć] 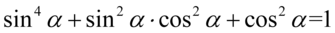
Lewa strona równości jest zdecydowanie dłuższa, zatem to ona będzie podlegać przekształceniom. Daną tożsamość można udowodnić na trzy sposoby:
I sposób
Aby najszybciej otrzymać prawą stronę należy pogrupować dwa początkowe składniki w nawias (jeżeli pomiędzy liczbami lub literami jest znak mnożenia to traktujemy to jako jeden element), a następnie wyciągnąć przed nawias największy wspólny czynnik. Zaczynamy od grupowania, wybraliśmy dwa pierwsze elementy, ponieważ przy sinusie jest wysoka potęga, a drugi składa się z sinusa i cosinusa, dlatego należy je „rozbroić”:
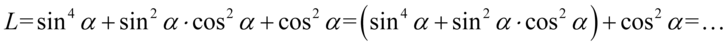
Wyciągamy największy wspólny czynnik przed nawias, tzn. 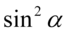 :
:
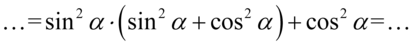
Przyjrzyjmy się dokładnie – w nawiasie powstała jedynka trygonometryczna:
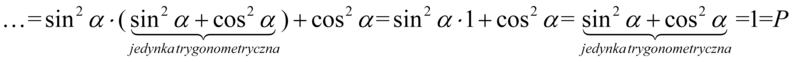
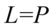
II sposób
Sposób ten jest nieco bardziej pracochłonny, polega on na zamianie wszelkich cosinusów na sinusy. Mamy ułatwione zadanie, ponieważ w przykładzie występuje tylko cosinus podniesiony do kwadratu, zatem można skorzystać z przekształconej jedynki trygonometrycznej  . Pamiętajmy o użyciu nawiasów, ponieważ czekają na nas kolejne działania:
. Pamiętajmy o użyciu nawiasów, ponieważ czekają na nas kolejne działania:
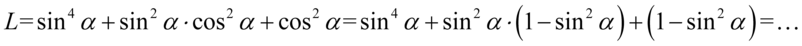
W tym momencie pozbędziemy się nawiasów: pierwszy wymnożymy przez 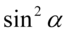 , a w przypadku drugiego opuszczamy nawias, ponieważ stoi przed nim znak dodawania:
, a w przypadku drugiego opuszczamy nawias, ponieważ stoi przed nim znak dodawania:

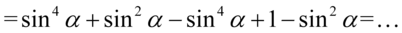
Na końcu redukujemy wyrazy podobne:
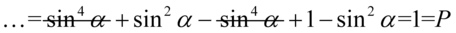
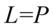
III sposób
Sposób ten jest analogiczny do drugiego, jednak tym razem wszelkie sinusy zastąpimy cosinusami. Na samym początku należy rozbroić 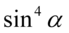 jeśli chcemy skorzystać z przekształconej jedynki trygonometrycznej – potrzebujemy
jeśli chcemy skorzystać z przekształconej jedynki trygonometrycznej – potrzebujemy 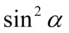 . Można tu zastosować własności potęg
. Można tu zastosować własności potęg 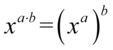 czyli
czyli 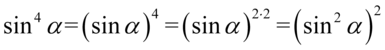 :
:

Teraz już bez problemu możemy skorzystać ze wzoru na przekształconą jedynkę trygonometryczną 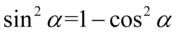 , pamiętajmy o użyciu nawiasów, ponieważ czekają nas inne działania:
, pamiętajmy o użyciu nawiasów, ponieważ czekają nas inne działania:
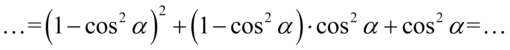
W celu pozbycia się pierwszego nawiasu, skorzystamy ze wzoru skróconego mnożenia 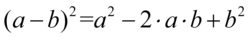 . Wynik zapiszemy w nawiasie „ochronnym”, żeby nie pogubić znaków, drugi nawias zlikwidujemy wymnażając go przez
. Wynik zapiszemy w nawiasie „ochronnym”, żeby nie pogubić znaków, drugi nawias zlikwidujemy wymnażając go przez 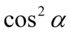 :
:
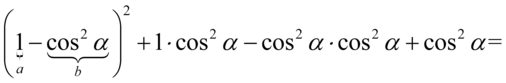
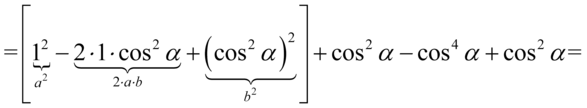
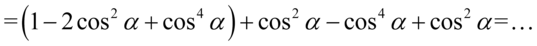
Likwidujemy nawias „ochronny” nie zmieniając żadnych znaków, ponieważ w domyśle stoi przed nim plus i po opuszczeniu nawiasu redukujemy wyrazy podobne:
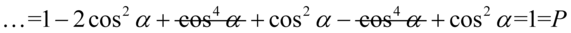
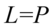
Przykład 124
[kliknij aby rozwinąć] 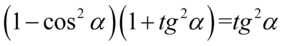
Lewa strona równości jest dłuższa, zatem to ona będzie przekształcana. Na początku przyjrzyjmy się zawartości pierwszego nawiasu, jest to przekształcona jedynka trygonometryczna 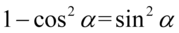 :
:
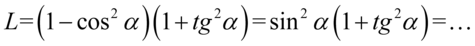
Teraz pozbędziemy się nawiasu wymnażając kolejno składniki:
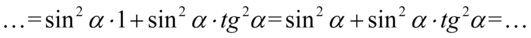
Na razie nie powstał żaden znajomy wzór, także jedynym wyjściem jest pozbycie się tangensa korzystając z formuły 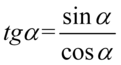 :
:
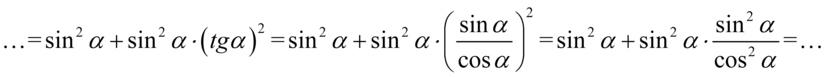
Teraz zgodnie z kolejnością działań należy wykonać mnożenie, dla ułatwienia zastosujemy zapis 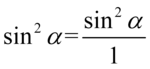 :
:
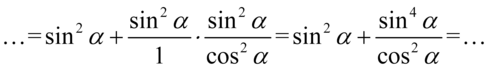
Powstały dwa wyrażenia, które sprowadzimy do wspólnego mianownika i znów dla ułatwienia działań użyjemy zapisu 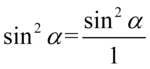 :
:
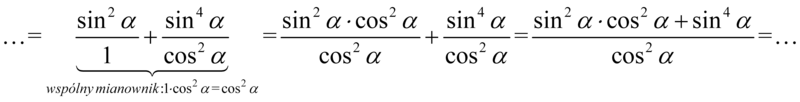
Kolejny krok to wyciągnięcie w liczniku przed nawias możliwie największego wspólnego elementu (czynnika), ponieważ nic więcej nie jesteśmy w stanie wykonać. Wyciągamy przed nawias 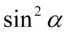 :
:
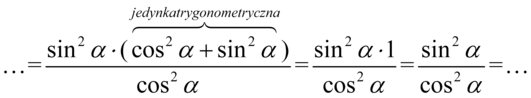
Aby otrzymać prawą stronę tożsamości musimy uzyskać 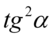 . W związku z tym najpierw skorzystamy z własności potęg
. W związku z tym najpierw skorzystamy z własności potęg 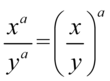 (w naszym przypadku
(w naszym przypadku 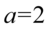 ):
):
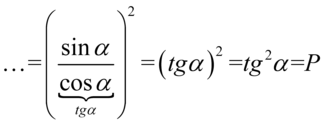
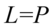
Przykład 125
[kliknij aby rozwinąć] 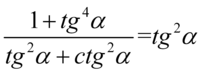
Założenie: 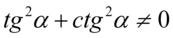 (mianownik ułamka nigdy nie może być równy
(mianownik ułamka nigdy nie może być równy  ). Po przeniesieniu otrzymujemy ostatecznie
). Po przeniesieniu otrzymujemy ostatecznie  .
.
Ponownie ostrzegam przed „radosnym” skracaniem w stylu: 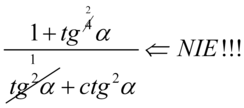 . Jest to niedopuszczalna operacja, ponieważ skracanie jest dozwolone tylko wtedy gdy znak dodawania wraz z otaczającymi go elementami jest zamknięty w nawiasie. Po nałożeniu nawiasu nie ma żadnych możliwości skracania
. Jest to niedopuszczalna operacja, ponieważ skracanie jest dozwolone tylko wtedy gdy znak dodawania wraz z otaczającymi go elementami jest zamknięty w nawiasie. Po nałożeniu nawiasu nie ma żadnych możliwości skracania 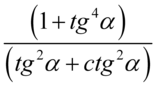 , a jak pamiętamy wnętrza nawiasu nie wolno ruszać.
, a jak pamiętamy wnętrza nawiasu nie wolno ruszać.
Lewa strona tożsamości jest zdecydowanie bardziej rozbudowana, także to ona będzie podlegać przekształceniom. Po prawej stronie do której uzyskania dążymy występuje tylko tangens, tak więc najbardziej oczywistym rozwiązaniem będzie zamiana cotangensa na tangens ze wzoru 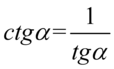 :
:
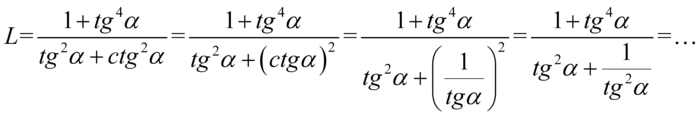
Teraz sprowadzimy do wspólnego mianownika dolne piętro dużego ułamka, dla ułatwienia zastosujemy zapis 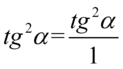 (każda liczba podzielona przez
(każda liczba podzielona przez 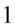 nie ulega zmianie):
nie ulega zmianie):
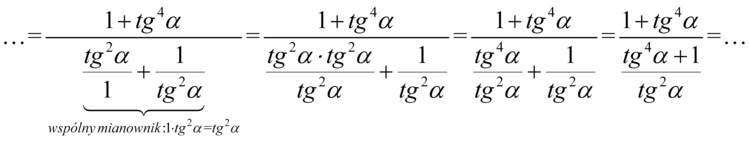
W tym momencie pozbędziemy się piętrowego ułamka zamieniając główną kreskę ułamkową na znak dzielenia, a następnie zamienimy dzielenie na mnożenie odwracając drugi składnik. Licznik weźmiemy w nawias ochronny, ponieważ dodawanie jest działaniem słabszym od dzielenia:
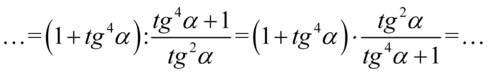
Aby nie było wątpliwości jak wykonać mnożenie użyjemy zapisu 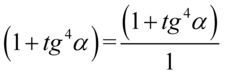 (każda liczba lub wyrażenie podzielone przez
(każda liczba lub wyrażenie podzielone przez 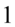 nie ulega zmianie):
nie ulega zmianie):
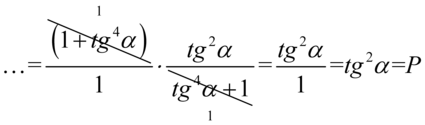
Skracanie było możliwe, ponieważ zawartość nawiasu i mianownik drugiego ułamka były identyczne.
Przykład 126
[kliknij aby rozwinąć] 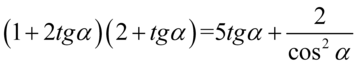
Założenie: 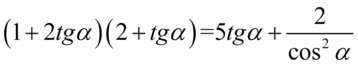 (mianownik nie może być równy
(mianownik nie może być równy  ). Po przekształceniu założenia otrzymujemy
). Po przekształceniu założenia otrzymujemy 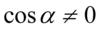 , ponieważ cosinus podniesiony do kwadratu jest różny od zera tylko wtedy gdy sam cosinus jest różny od zera.
, ponieważ cosinus podniesiony do kwadratu jest różny od zera tylko wtedy gdy sam cosinus jest różny od zera.
Zajmiemy się lewą stroną, ponieważ znajdują się tam nawiasy, które łatwiej jest zlikwidować niż uzyskać. Zaczynamy od pozbycia się nawiasów wymnażając kolejno elementy:
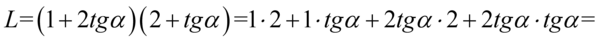
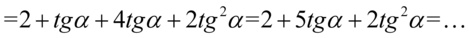
Właściwie otrzymaliśmy już część prawej strony tożsamości, a mianowicie 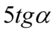 , dlatego tego zapisu nie będziemy już przekształcać, a
, dlatego tego zapisu nie będziemy już przekształcać, a 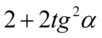 musimy doprowadzić do postaci
musimy doprowadzić do postaci 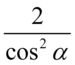 . Zamieńmy kolejność składników tak aby
. Zamieńmy kolejność składników tak aby 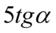 znajdowało się na początku:
znajdowało się na początku:
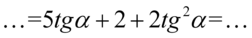
Aby uzyskać cosinus skorzystamy ze wzoru 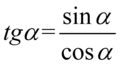 :
:
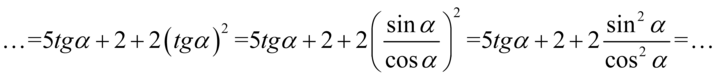
W celu ułatwienia dalszych działań zastosujemy zapis 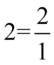 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez 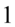 nie ulega zmianie:
nie ulega zmianie:
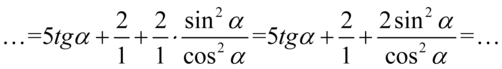
Teraz sprowadzimy powstałe ułamki do wspólnego mianownika:
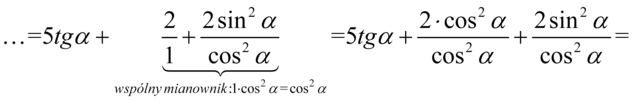
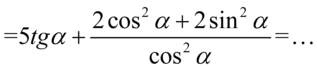
Jeżeli wyciągniemy dwójkę przed nawias w liczniku, to otrzymamy w nawiasie jedynkę trygonometryczną: