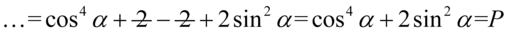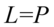Przykład 119
[kliknij aby rozwinąć] 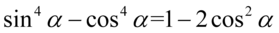
W tym przykładzie obie strony mają podobną długość, jednak po lewej stronie występują wyższe wartości potęg i to właśnie lewa strona będzie przekształcana. Trzeba się tu również wykazać znajomością wzorów skróconego mnożenia. Na początku zapiszemy czwórki z wykładników potęg za pomocą dwójek, ponieważ po prawej stronie znajdują się właśnie dwójki:

Teraz skorzystamy z własności potęg, gdzie 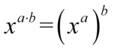 :
:
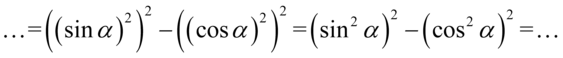
Przyjrzyjmy się powstałemu wynikowi - mamy dwa elementy poniesione do kwadratu, które są oddzielone znakiem minus. I w tym momencie trzeba użyć wzoru skróconego mnożenia 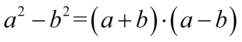 do rozłożenia powstałego wyrażenia na czynniki (czyli iloczyn nawiasów):
do rozłożenia powstałego wyrażenia na czynniki (czyli iloczyn nawiasów):
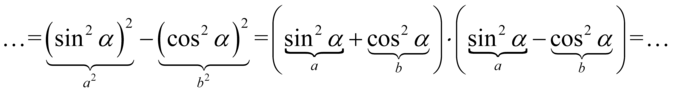
Teraz przyjrzyjmy się zawartości nawiasów, w pierwszym z nich otrzymaliśmy jedynkę trygonometryczną:
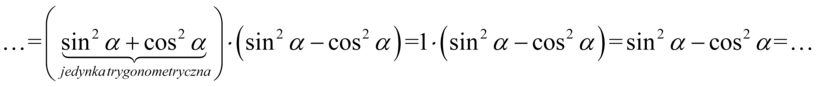
Po prawej stronie nie występuje 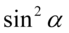 , tak więc przekształcimy go na cosinus stosując wzór na przekształconą jedynkę trygonometryczną
, tak więc przekształcimy go na cosinus stosując wzór na przekształconą jedynkę trygonometryczną 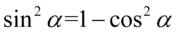 , nie zapominajmy o nawiasach:
, nie zapominajmy o nawiasach:
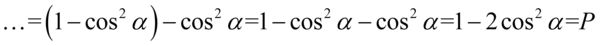
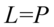
Przykład 120
[kliknij aby rozwinąć] 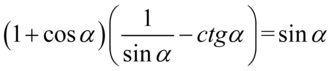
Założenie: 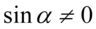 (mianownik nie może być równy
(mianownik nie może być równy  )
)
Lewa strona równości jest dłuższa, zatem to ona będzie przekształcana. Zaczniemy od opuszczenia nawiasów i wymnożymy kolejno elementy:
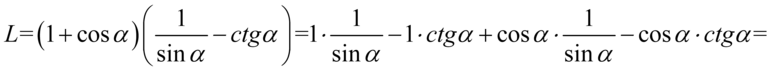
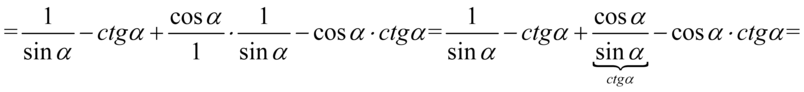

Dla ułatwienia działań zastosowano zapis 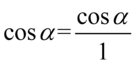 , dzięki któremu zyskaliśmy pewność jakie elementy można ze sobą wymnożyć.
, dzięki któremu zyskaliśmy pewność jakie elementy można ze sobą wymnożyć.
Kolejny krok to likwidacja cotangensa, ponieważ po prawej stronie do której uzyskania dążymy tangens nie występuje. Korzystamy oczywiście ze wzoru 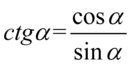 :
:
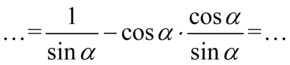
Tu ponownie skorzystamy z zapisu 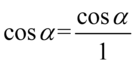 dla ułatwienia działań:
dla ułatwienia działań:
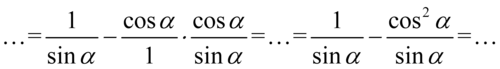
Uzyskaliśmy wspólny mianownik, dlatego można bez obaw zapisać oba ułamki na jednej kresce ułamkowej:
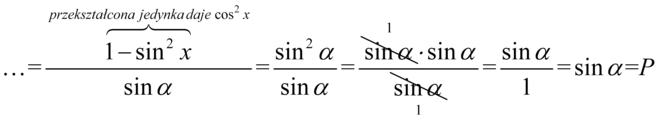
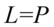
Przykład 121
[kliknij aby rozwinąć] 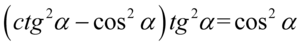
Lewa strona równości jest dłuższa, zatem to ona będzie podlegać przekształceniom. Zaczniemy od opuszczeni nawiasów wymnażając kolejno składniki:
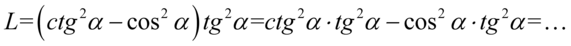
Teraz przyjrzyjmy się zapisowi 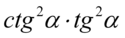 . Przypomina on nieco wzór
. Przypomina on nieco wzór 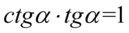 , ale kwadraty nie pozwalają nam od razu zastąpić go jedynką. Nie stanowi to problemu, ponieważ korzystając z własności potęg mamy
, ale kwadraty nie pozwalają nam od razu zastąpić go jedynką. Nie stanowi to problemu, ponieważ korzystając z własności potęg mamy 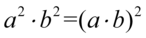 :
:
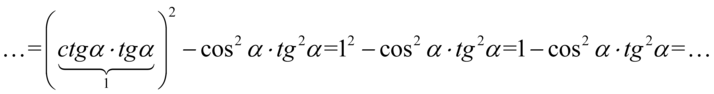
Kolejny etapem będzie likwidacja tangensa przy użyciu wzoru 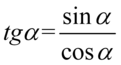 :
:
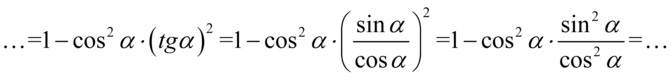
Dla ułatwienia działań zastosujemy zapis 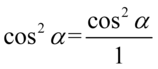 , dzięki któremu zyskamy pewność jakie elementy można ze sobą skracać:
, dzięki któremu zyskamy pewność jakie elementy można ze sobą skracać:
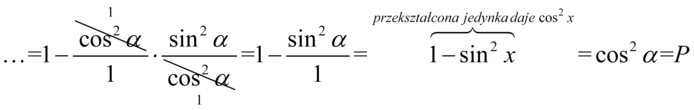
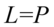
Przykład 122
[kliknij aby rozwinąć] 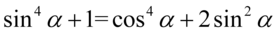
Daną równość można udowodnić na dwa sposoby.
I sposób
Zajmiemy się prawą stroną, którą należy przekształcić w podobny zapis znajdujący się po lewej stronie. Zwróćmy uwagę na większą potęgę, która jest przy cosinusie. Na początku zlikwidujemy wykładnik  na niższy korzystając z własności potęg
na niższy korzystając z własności potęg 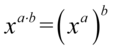 czyli
czyli 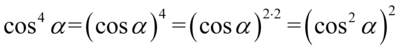 :
:
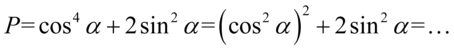
Teraz przekształcimy cosinus znajdujący się w nawiasie na sinus korzystając z przekształconej jedynki trygonometrycznej  :
:
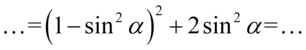
Następnie pozbędziemy się nawiasu korzystając ze wzoru skróconego mnożenia 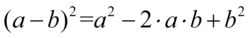 . Wynik zapiszemy w nawiasie aby nie pogubić znaków, ponieważ oprócz zlikwidowania nawiasów mamy do wykonania inne działania:
. Wynik zapiszemy w nawiasie aby nie pogubić znaków, ponieważ oprócz zlikwidowania nawiasów mamy do wykonania inne działania:

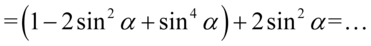
Teraz pozbędziemy się nawiasów. Przed nawiasem nie ma nic, a więc w domyśle jest plus, także opuszczając nawias nie zmieniamy żadnych znaków, a następnie zredukujemy wyrazy podobne:
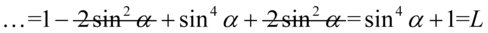
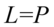
II sposób
Zajmiemy się lewą stroną. Tu znowu zwróćmy uwagę na większą potęgę, która znajduje się tym razem przy sinusie. Po prawej stronie mamy sinus z niższą potęgą, tak więc na początku zlikwidujemy wykładnik  na niższy korzystając z własności potęg
na niższy korzystając z własności potęg 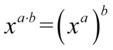 czyli
czyli 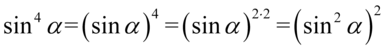 :
:
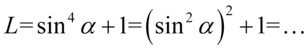
Teraz przekształcimy sinus znajdujący się w nawiasie na cosinus korzystając z przekształconej jedynki trygonometrycznej 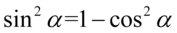 :
:
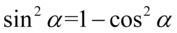
Następnie pozbędziemy się nawiasu korzystając ze wzoru skróconego mnożenia 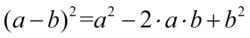 . Wynik zapiszemy w nawiasie aby nie pogubić znaków, ponieważ oprócz zlikwidowania nawiasów mamy do wykonania inne działania:
. Wynik zapiszemy w nawiasie aby nie pogubić znaków, ponieważ oprócz zlikwidowania nawiasów mamy do wykonania inne działania:
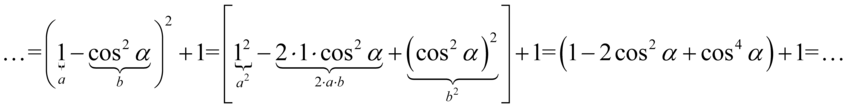
Teraz pozbędziemy się nawiasów. Przed nawiasem nie ma nic, a więc w domyśle jest plus, także opuszczając nawias nie zmieniamy żadnych znaków, a następnie zredukujemy wyrazy podobne:
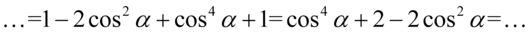
Mamy już 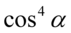 , który znajduje się po prawej stronie, ale potrzebujemy jeszcze
, który znajduje się po prawej stronie, ale potrzebujemy jeszcze 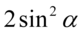 . Możemy łatwo pozbyć się cosinusa korzystając ze wzoru na przekształconą jedynkę trygonometryczną
. Możemy łatwo pozbyć się cosinusa korzystając ze wzoru na przekształconą jedynkę trygonometryczną  . Nie zapominajmy o użyciu nawiasów:
. Nie zapominajmy o użyciu nawiasów:
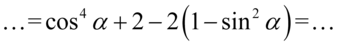
Ponownie pozbędziemy się nawiasów wymnażając dwójkę: