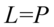Przykład 115
[kliknij aby rozwinąć] 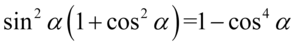
Dany przykład można udowodnić na dwa sposoby.
I sposób
Zajmiemy się lewą stroną i zaczniemy niestandardowo – nie będziemy pozbywać się nawiasów, ponieważ i tak to nic nie da. Po prawej stronie do której otrzymania dążymy występuje wyłącznie cosinus, także pierwszym krokiem będzie zamiana sinusa z lewej strony tożsamości na cosinus. Skorzystamy tu z przekształconej jedynki trygonometrycznej 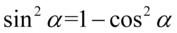 , nie zapominajmy o użyciu nawiasów:
, nie zapominajmy o użyciu nawiasów:
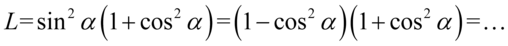
Dopiero teraz pozbędziemy się nawiasów. Przyjrzymy się ich zawartości – jest właściwie identyczna oprócz znaku. Dzięki temu można skorzystać ze wzoru skróconego mnożenia 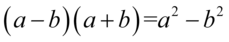 . Oczywiście nie się nie stanie jeśli wymnożymy nawiasy na piechotę, ale będzie to trwało nieco dłużej:
. Oczywiście nie się nie stanie jeśli wymnożymy nawiasy na piechotę, ale będzie to trwało nieco dłużej:
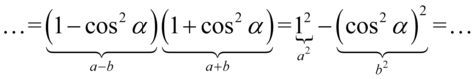
Na końcu skorzystamy z właściwości potęg 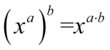 i otrzymujemy:
i otrzymujemy:
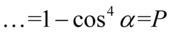
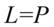
II sposób
Tym razem zajmiemy się prawą stroną i od razu skorzystamy ze wzoru skróconego mnożenia 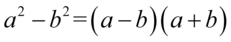 , ponieważ po tej stronie mamy dwa elementy podniesione do parzystych potęg oddzielone minusem. Należy się zastanowić co podniesione do kwadratu daje
, ponieważ po tej stronie mamy dwa elementy podniesione do parzystych potęg oddzielone minusem. Należy się zastanowić co podniesione do kwadratu daje 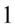 i
i 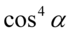 :
:
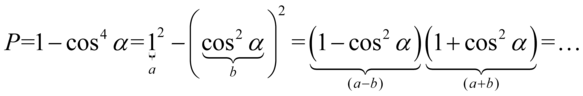
Na końcu skorzystamy ze wzoru na przekształconą jedynkę trygonometryczną 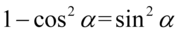 :
:
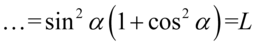
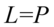
Przykład 116
[kliknij aby rozwinąć] 
Daną tożsamość można udowodnić na dwa sposoby.
I sposób
Zajmiemy się lewą stroną, którą należy przekształcić w bardzo podobny zapis. Zwróćmy uwagę na większą potęgę, która jest przy cosinusie. Po prawej stronie mamy już cosinus do kwadratu, a więc musimy ją rozpisać. Na początku zlikwidujemy wykładnik 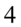 na niższy korzystając z własności potęg
na niższy korzystając z własności potęg 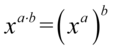 czyli
czyli 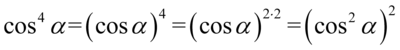 :
:
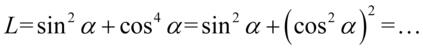
Teraz przekształcimy cosinus znajdujący się w nawiasie na sinus korzystając z przekształconej jedynki trygonometrycznej  :
:
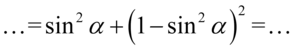
Następnie pozbędziemy się nawiasu korzystając ze wzoru skróconego mnożenia 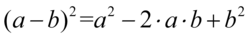 . Wynik zapiszemy w nawiasie aby nie pogubić znaków, ponieważ oprócz zlikwidowania nawiasów mamy do wykonania inne działania:
. Wynik zapiszemy w nawiasie aby nie pogubić znaków, ponieważ oprócz zlikwidowania nawiasów mamy do wykonania inne działania:
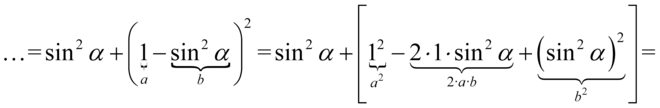

Teraz pozbędziemy się nawiasów. Przed nawiasem jest znak plus także opuszczając nawias nie zmieniamy żadnych znaków, a następnie zredukujemy wyrazy podobne:
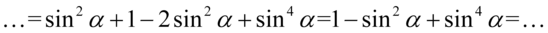
Otrzymaliśmy sinus podniesiony do potęgi czwartej, ale po prawej stronie oprócz tego musimy uzyskać 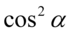 , także należy zlikwidować
, także należy zlikwidować 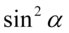 . Tu ponownie skorzystamy z przekształconej jedynki trygonometrycznej
. Tu ponownie skorzystamy z przekształconej jedynki trygonometrycznej 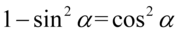 :
:
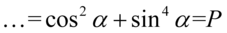
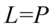
II sposób
Zajmiemy się prawą stroną, którą należy przekształcić w bardzo podobny zapis. Zwróćmy uwagę na większą potęgę, która jest przy sinusie. Po lewej stronie mamy już sinus do kwadratu, a więc musimy ją rozpisać. Na początku zlikwidujemy wykładnik 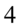 na niższy korzystając z własności potęg
na niższy korzystając z własności potęg 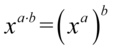 czyli
czyli 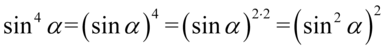 :
:
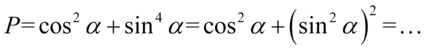
Teraz przekształcimy sinus znajdujący się w nawiasie na cosinus korzystając z przekształconej jedynki trygonometrycznej 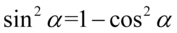 :
:
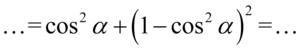
Następnie pozbędziemy się nawiasu korzystając ze wzoru skróconego mnożenia 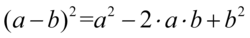 . Wynik zapiszemy w nawiasie aby nie pogubić znaków, ponieważ oprócz zlikwidowania nawiasów mamy do wykonania inne działania:
. Wynik zapiszemy w nawiasie aby nie pogubić znaków, ponieważ oprócz zlikwidowania nawiasów mamy do wykonania inne działania:
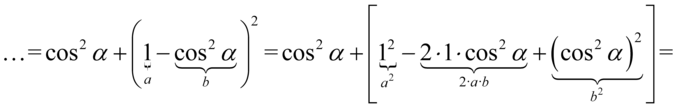
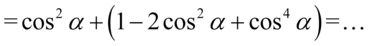
Teraz pozbędziemy się nawiasów. Przed nawiasem jest znak plus także opuszczając nawias nie zmieniamy żadnych znaków, a następnie zredukujemy wyrazy podobne:
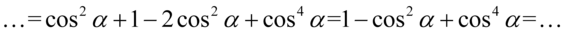
Otrzymaliśmy cosinus podniesiony do potęgi czwartej, ale po lewej stronie oprócz tego musimy uzyskać 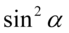 , także należy zlikwidować
, także należy zlikwidować 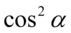 . Tu ponownie skorzystamy z przekształconej jedynki trygonometrycznej
. Tu ponownie skorzystamy z przekształconej jedynki trygonometrycznej 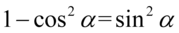 :
:
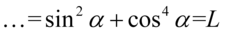
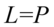
Przykład 117
[kliknij aby rozwinąć] 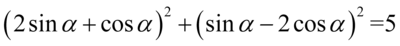
Lewa strona równości jest zdecydowanie dłuższa, zatem to ona będzie przekształcana. Zaczniemy od likwidacji nawiasów korzystając ze wzorów skróconego mnożenia 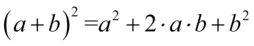 do pierwszego nawiasu oraz
do pierwszego nawiasu oraz 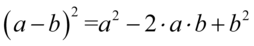 do drugiego. Wyniki obydwu przekształceń zapiszemy w nawiasach, ponieważ mamy w perspektywie wykonywanie dalszych działań (dodawanie) i dzięki temu unikniemy niebezpieczeństwa polegającego na zgubieniu znaków:
do drugiego. Wyniki obydwu przekształceń zapiszemy w nawiasach, ponieważ mamy w perspektywie wykonywanie dalszych działań (dodawanie) i dzięki temu unikniemy niebezpieczeństwa polegającego na zgubieniu znaków:


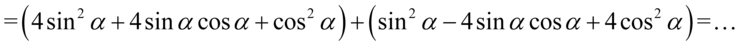
W tym momencie pozbędziemy się nawiasów „ochronnych” - znajduje się przed nimi znak dodawania (nawet jeśli go nie widać), także opuszczając nawiasy nic się nie zmienia w ich zawartości:
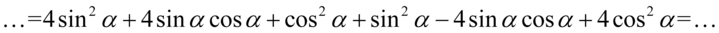
Po opuszczeniu nawiasów zredukujemy wyrazy podobne:

Kończąc dowodzenie prawdziwości tożsamości wyciągniemy 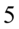 przed nawias, która dosłownie się o to prosi i dzięki temu zapisujemy
przed nawias, która dosłownie się o to prosi i dzięki temu zapisujemy 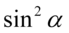 oraz
oraz 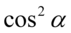 obok siebie, co daje jedynkę trygonometryczną:
obok siebie, co daje jedynkę trygonometryczną:
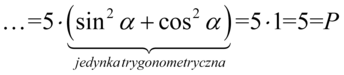
Przykład 118
[kliknij aby rozwinąć] 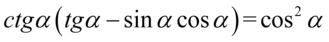
Lewa strona przykładu jest dłuższa, zatem to ona będzie podlegać przekształceniom. Na samym początku pozbędziemy się nawiasów wymnażając kolejno składniki:
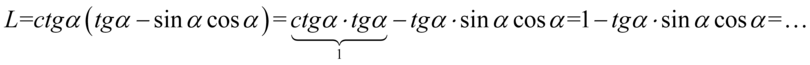
Teraz pozbędziemy się tangensa korzystając ze wzoru 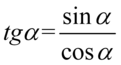 , ponieważ po prawej stronie do której uzyskania dążymy tangens nie występuje:
, ponieważ po prawej stronie do której uzyskania dążymy tangens nie występuje:
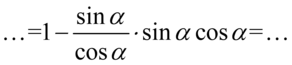
W tym momencie możemy skrócić poszczególne wyrażenia, ponieważ pomiędzy nimi występuje wyłącznie znak mnożenia. Aby bezbłędnie wykonać skracanie zastosujemy zapis 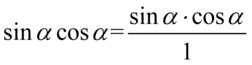 , ponieważ jakakolwiek liczba podzielona przez
, ponieważ jakakolwiek liczba podzielona przez 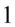 nie ulega zmianie:
nie ulega zmianie: