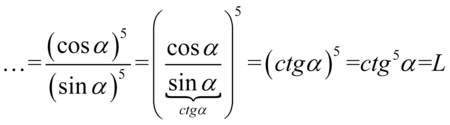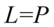Przykład 113
[kliknij aby rozwinąć] 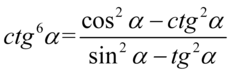
Założenie: 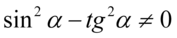 (mianownik nie może być równy zero)
(mianownik nie może być równy zero)
Prawa strona różności jest wyraźnie dłuższa, zatem to ona będzie podlegać przekształceniom. Na początku pozbędziemy się tangensa i cotangensa ze wzorów 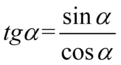 oraz
oraz 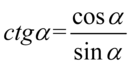 . Zlikwidowanie tych elementów może się wydać dziwne, ponieważ po lewej stronie tożsamości do której otrzymania dążymy występuje cotangens, ale w tym przypadku nie mamy za bardzo innych możliwości rozpoczęcia sensownych przekształceń:
. Zlikwidowanie tych elementów może się wydać dziwne, ponieważ po lewej stronie tożsamości do której otrzymania dążymy występuje cotangens, ale w tym przypadku nie mamy za bardzo innych możliwości rozpoczęcia sensownych przekształceń:
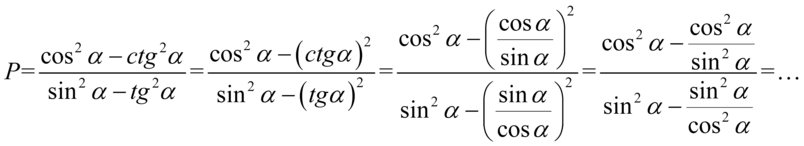
Teraz spróbujemy każde piętro dużego ułamka zapisać jako jeden ułamek poprzez sprowadzenie do wspólnego mianownika, dla ułatwienia zastosujemy zapis 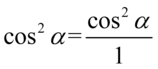 oraz
oraz 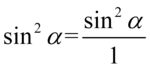 (każda liczba lub wyrażenie podzielone przez
(każda liczba lub wyrażenie podzielone przez 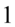 nie ulega zmianie):
nie ulega zmianie):
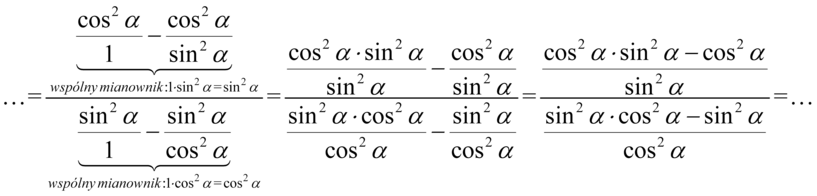
Kolejny krok to zlikwidowanie piętrowego ułamka poprzez zamianę głównej kreski ułamkowej na znak dzielenia, a później zmiana dzielenia na mnożenie przez odwrotność drugiego ułamka:
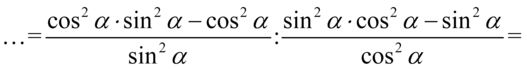
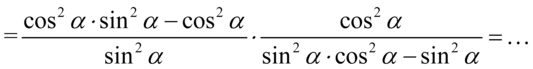
Na tym etapie skracanie nie jest możliwe, ponieważ w liczniku pierwszego ułamka i mianowniku drugiego występuje minus, który wraz z otaczającymi go składnikami nie jest zamknięty w nawiasie. Warto zauważyć, że w liczniku pierwszego ułamka i mianowniku drugiego mamy powtarzające się elementy tzn. 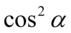 w pierwszym oraz
w pierwszym oraz 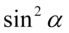 w drugim, można zatem wyciągnąć je przed nawias. Pamiętajmy, że przy zabraniu wszystkiego przy wyłączaniu wspólnego czynnika przed nawias zawsze zostaje
w drugim, można zatem wyciągnąć je przed nawias. Pamiętajmy, że przy zabraniu wszystkiego przy wyłączaniu wspólnego czynnika przed nawias zawsze zostaje 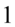 :
:
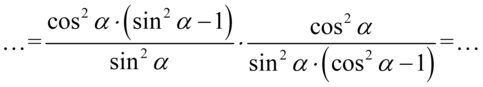
Niestety ze skracania nici – ani na skos, ani góra – dół, pamiętajmy, że wnętrza nawiasów nie wolno skracać (nawias skracany jest jako całość z innym identycznym nawiasem). Wymnóżmy zatem cosinusy z liczników i sinusy z mianowników, żeby nieco „skompresować” wyrażenie, czyli licznik razy licznik, mianownik razy mianownik – tak jak przy zwyczajnym mnożeniu ułamków zwykłych:
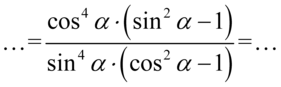
Teraz przyjrzyjmy się zawartości nawiasów, bardzo przypominają one wzory na przekształconą jedynkę trygonometryczną tzn. 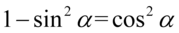 oraz
oraz 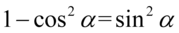 tylko różnią się kolejnością składników, tak więc zmieńmy tą kolejność. Oczywiście pamiętamy, że liczba lub wyrażenie tworzy całość wraz z poprzedzającym go znakiem i przy zmianie kolejności trzeba brać pod uwagę tenże znak i także go przenosić:
tylko różnią się kolejnością składników, tak więc zmieńmy tą kolejność. Oczywiście pamiętamy, że liczba lub wyrażenie tworzy całość wraz z poprzedzającym go znakiem i przy zmianie kolejności trzeba brać pod uwagę tenże znak i także go przenosić:
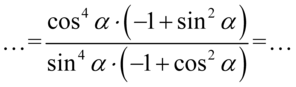
Niestety zawartość nawiasów różni się od wzorów na przekształconą jedynkę trygonometryczną, ale teraz już tylko znakami. Jeżeli zaszła taka sytuacja to należy wyciągnąć minus przed nawias, a wtedy otrzymamy pożądany wynik. Przy wyciąganiu minusa znaki w nawiasie zmienią się na przeciwne, a minus powędruje dla wygody na początek przykładu (jest to dozwolone tylko w przypadku elementów wymnożonych przez nawias):

Wymnóżmy powstałe elementy, pamiętając oczywiście, że wykładniki się dodaje i skróćmy minusy:

Utworzyła się potęga o wykładniku równym 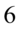 , co jest zgodne z lewą stroną tożsamości, ale potrzebujemy jeszcze cotangensa do końcowego wyniku. Skorzystamy z własności potęg
, co jest zgodne z lewą stroną tożsamości, ale potrzebujemy jeszcze cotangensa do końcowego wyniku. Skorzystamy z własności potęg  i korzystając na końcu ze wzoru
i korzystając na końcu ze wzoru  otrzymujemy lewą stronę tożsamości:
otrzymujemy lewą stronę tożsamości:
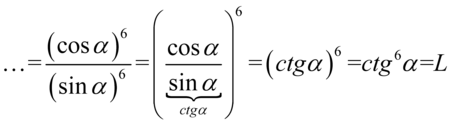
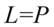
Przykład 114
[kliknij aby rozwinąć] 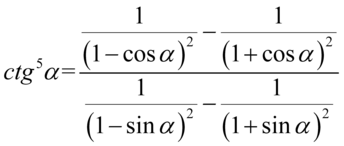
Założenie: 
(żaden z mianowników nie może być równy zero). Jak widać w założeniu nie uwzględniono kwadratów mianowników. Nie ma takiej potrzeby, ponieważ to zawartość nawiasu decyduje czy mianownik będzie różny od zera.
Prawa strona równości jest zdecydowanie dłuższa, zatem to ona będzie podlegać przekształceniom. W tym przypadku trzeba wykazać się sprytem, ponieważ nieumiejętne przekształcanie może skomplikować przykład. Zamiast pozbywania się nawiasów na samym początku sprowadźmy ułamki z poszczególnych pięter do wspólnego mianownika:
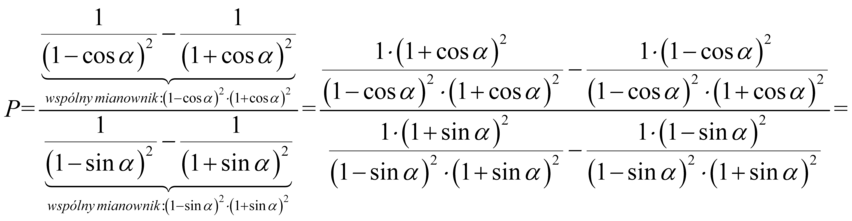
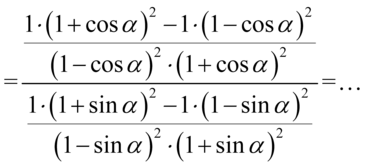
Pozbędziemy się jedynek wymnożonych przez nawiasy w licznikach powstałych ułamków, ponieważ każda liczba lub znak wymnożona przez  nie ulega zmianie:
nie ulega zmianie:
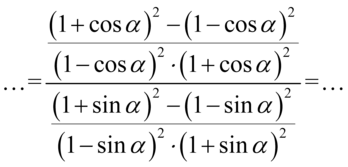
Teraz sprytnie uprościmy mianowniki obydwu ułamków, oczywiście można podnosić zawartość nawiasów ze wzorów skróconego mnożenia, a następnie wymnażać, ale będzie to zdecydowanie dłuższa i mniej przyjemna droga. W obu przypadkach mamy zapis 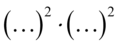 , gdzie wykładniki potęg są identyczne. Korzystając z własności działań na potęgach
, gdzie wykładniki potęg są identyczne. Korzystając z własności działań na potęgach 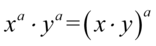 otrzymujemy
otrzymujemy 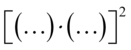 , a więc:
, a więc:
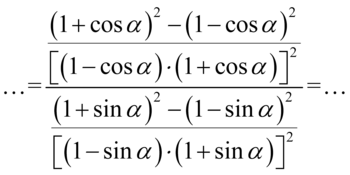
W tym momencie warto przyjrzeć się zawartości nawiasów kwadratowych. W każdym z nich znajdują się wymnożone przez siebie dwa nawiasy różniące się tylko znakiem w środku – w związku z tym można zastosować wzór skróconego mnożenia 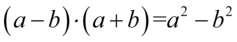 . Oczywiście nic się nie stanie, jeśli nie zauważymy tego wzoru i wymnożymy nawias przez nawias „na piechotę”:
. Oczywiście nic się nie stanie, jeśli nie zauważymy tego wzoru i wymnożymy nawias przez nawias „na piechotę”:


Ostatecznie w mianownikach ponownie skorzystamy z własności potęg 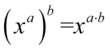 i otrzymamy:
i otrzymamy:
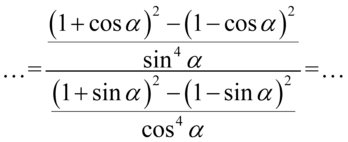
Czas uprościć liczniki ułamków w poszczególnych pięter. Skorzystamy tu ze wzorów skróconego mnożenia postaci 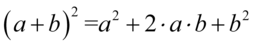 oraz
oraz 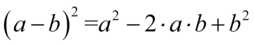 . Wyniki rozwinięcia wzorów zapiszemy w nawiasach, ponieważ czeka nas jeszcze odejmowanie. Robimy to w celu ochrony przez zgubieniem znaków:
. Wyniki rozwinięcia wzorów zapiszemy w nawiasach, ponieważ czeka nas jeszcze odejmowanie. Robimy to w celu ochrony przez zgubieniem znaków:
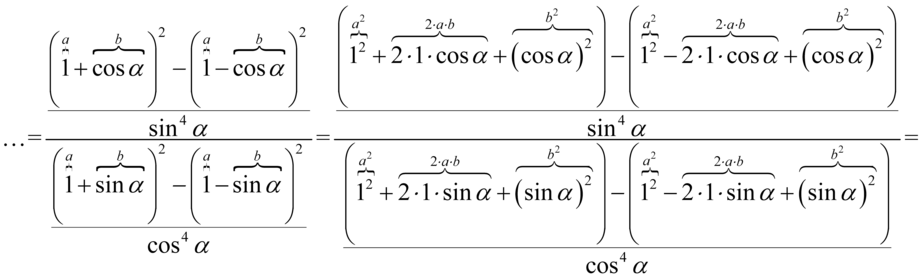
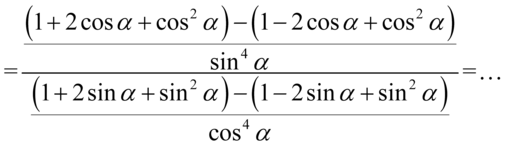
Teraz opuścimy nawiasy – tam, gdzie przed nawiasem nie ma żadnego znaku stoi w domyśle plus, czyli opuszczamy nawiasy bez zmiany znaków w środku. Z kolei przed drugim nawiasem stoi minus, tak więc opuszczając nawias zmieniamy wszystkie znaki z wnętrza nawiasu na przeciwne:
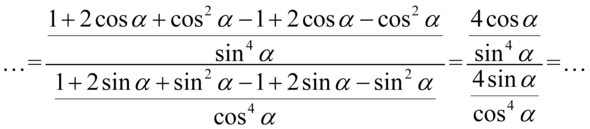
W tym momencie nie ma możliwości uproszczenia ułamków z poszczególnych pięter, tak więc pozbędziemy się piętrowego ułamka zastępując główną kreską ułamkową znakiem dzielenia, a następnie zamienimy dzielenie na mnożenie odwracając drugi ułamek:
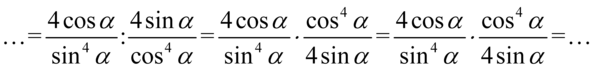
Skrócenie 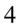 było możliwe, ponieważ pomiędzy składnikami w obu ułamkach występują wyłącznie znak mnożenia. Gdyby komuś przyszło do głowy skrócenie potęg to znów przestrzegam – nie wolno! Jak widać reszta elementów nie jest skracalna i zostaje wymnożenie licznika przez licznik, mianownik przez mianownik:
było możliwe, ponieważ pomiędzy składnikami w obu ułamkach występują wyłącznie znak mnożenia. Gdyby komuś przyszło do głowy skrócenie potęg to znów przestrzegam – nie wolno! Jak widać reszta elementów nie jest skracalna i zostaje wymnożenie licznika przez licznik, mianownik przez mianownik:
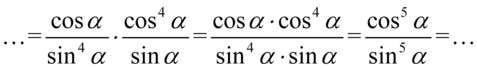
Kończąc przykład zastosujemy własności potęg 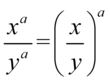 i wzór
i wzór 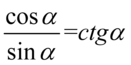 :
: