Przykład 112
[kliknij aby rozwinąć] 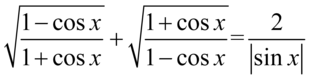
Założenie: 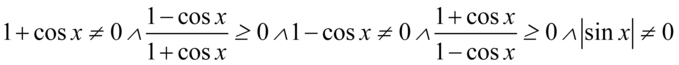
Żaden z mianowników musi być różny od zera, a wyrażenia znajdujące się pod pierwiastkiem muszą mieć wartość większą bądź równą od zera.
Od razu przestrzegam przed skracaniem typu 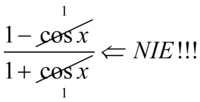 lub
lub 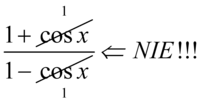 lub wyciąganiem pierwiastków
lub wyciąganiem pierwiastków 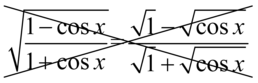 . Jeżeli pod pierwiastkiem znajduje się dodawanie lub odejmowanie, to nie można rozdzielać wrażenia podpierwiastkowego na dwa oddzielne!
. Jeżeli pod pierwiastkiem znajduje się dodawanie lub odejmowanie, to nie można rozdzielać wrażenia podpierwiastkowego na dwa oddzielne!
Lewa strona tożsamości jest dłuższa, zatem to ona będzie podlegać przekształceniom. W przykładzie nie ma niestety żadnych charakterystycznych wzorów, które pozwolą na jego uproszczenie, można oczywiście rozpisać jedynki ze wzoru 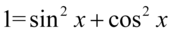 , ale i tak to nic nie da. Uprzedzam też przed zapisaniem obydwu ułamków pod jedną kreską ułamkową,a więc
, ale i tak to nic nie da. Uprzedzam też przed zapisaniem obydwu ułamków pod jedną kreską ułamkową,a więc 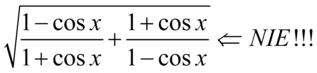 - jest to działanie niedozwolone. Jeżeli pomiędzy dwoma pierwiastkami znajduje się znak dodawania lub odejmowania nie wolno wyrażeń podpierwiastkowych zapisać pod jednym pierwiastkiem
- jest to działanie niedozwolone. Jeżeli pomiędzy dwoma pierwiastkami znajduje się znak dodawania lub odejmowania nie wolno wyrażeń podpierwiastkowych zapisać pod jednym pierwiastkiem  .
.
W przykładzie tym trzeba użyć pewnego triku tzn. domnożyć liczniki lub mianowniki obydwu ułamków przez wyrażenie z przeciwnym znakiem, aby otrzymać przekształconą jedynkę trygonometryczną. Zostaną przedstawione dwa sposoby – pierwszy z domnożeniem mianownika i drugi (nieco dłuższy) z domnożeniem licznika.
I sposób
Zaczniemy od wymnożenia mianowników obydwu ułamków przez wyrażenie z przeciwnym znakiem, oczywiście identyczne wyrażenie trzeba dopisać w liczniku, ponieważ tylko wtedy nie zmieni się wartość ułamka. Pamiętajmy o używaniu nawiasów, lepiej napisać ich więcej niż mniej:
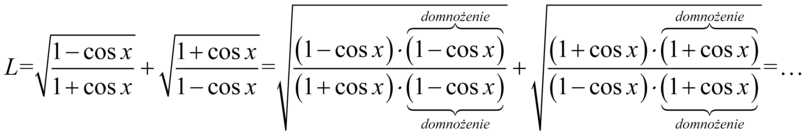
Teraz uprościmy obydwa mianowniki pozbywając się nawiasów. Można to zrobić „na piechotę” kolejno wymnażając składniki lub stosując wzór skróconego mnożenia 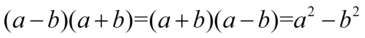 , ponieważ w obu ułamkach zawartość nawiasów różni się tylko znakiem w środku, co jest charakterystyczne dla podanego wzoru. Natomiast liczniki zapiszemy w nieco prostszej postaci – w obu ułamkach powstały dwa identyczne nawiasy wymnożone przez siebie, a więc
, ponieważ w obu ułamkach zawartość nawiasów różni się tylko znakiem w środku, co jest charakterystyczne dla podanego wzoru. Natomiast liczniki zapiszemy w nieco prostszej postaci – w obu ułamkach powstały dwa identyczne nawiasy wymnożone przez siebie, a więc 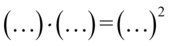 :
:
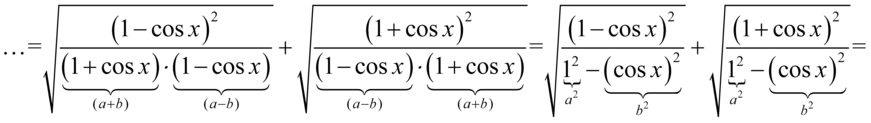
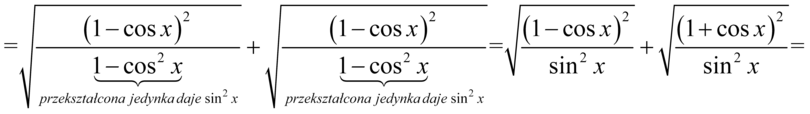
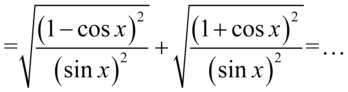
Kolejny etap stanowi likwidacja pierwiastków i tutaj niezbędna okaże się znajomość wzorów związanych z wartością bezwzględną. Na początku skorzystamy z własności działań na pierwiastkach tzn. 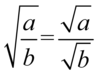 i wejdziemy z pierwiastkami w obydwu ułamkach w licznik i mianownik :
i wejdziemy z pierwiastkami w obydwu ułamkach w licznik i mianownik :
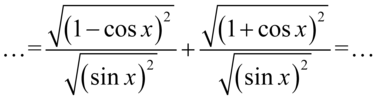
Teraz skorzystamy z własności 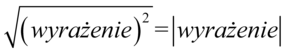 , co wyjaśnia, dlaczego nawiasy w licznikach obydwu ułamków nie był wcześniej wymnażane tylko sprowadzone do nawiasów podniesionych do kwadratu :
, co wyjaśnia, dlaczego nawiasy w licznikach obydwu ułamków nie był wcześniej wymnażane tylko sprowadzone do nawiasów podniesionych do kwadratu :
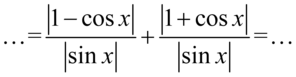
Kolejnym krokiem będzie likwidacja wartości bezwzględnej (modułu) tam, gdzie jest to możliwe bez dodatkowych założeń, które jak widać nie były podane w przykładzie. Do tego niezbędna jest znajomość wartości, jakie osiąga funkcja sinus i cosinus. Sinus, a także cosinus osiągają wartości wyłącznie ze zbioru 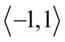 , czyli sinus i cosinus może być liczbą od
, czyli sinus i cosinus może być liczbą od 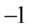 do
do 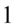 włącznie. Jakie ma to znaczenie dla modułów? Przeanalizujmy każdy z osobna.
włącznie. Jakie ma to znaczenie dla modułów? Przeanalizujmy każdy z osobna.
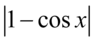 - jeżeli zamiast cosinusa wstawimy dowolną liczbę z przedziału
- jeżeli zamiast cosinusa wstawimy dowolną liczbę z przedziału 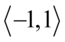 to zawsze w module otrzymamy wartość równą
to zawsze w module otrzymamy wartość równą  lub większą od zera. Sprawdźmy więc kilka przykładowych liczb:
lub większą od zera. Sprawdźmy więc kilka przykładowych liczb:
np. 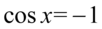 i wtedy
i wtedy 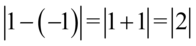 czyli
czyli 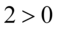
np. 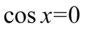 i wtedy
i wtedy 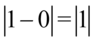 czyli
czyli 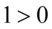
np. 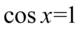 i wtedy
i wtedy  czyli
czyli 
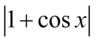 - jeżeli zamiast cosinusa wstawimy dowolną liczbę z przedziału
- jeżeli zamiast cosinusa wstawimy dowolną liczbę z przedziału 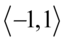 to zawsze w module otrzymamy wartość równą
to zawsze w module otrzymamy wartość równą  lub większą od zera. Sprawdźmy więc kilka przykładowych liczb:
lub większą od zera. Sprawdźmy więc kilka przykładowych liczb:
np. 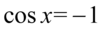 i wtedy
i wtedy 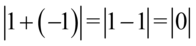 czyli
czyli 
np. 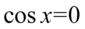 i wtedy
i wtedy 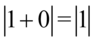 czyli
czyli 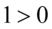
np. 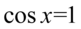 i wtedy
i wtedy  czyli
czyli 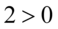
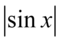 - jeżeli zamiast sinusa wstawimy dowolną liczbę z przedziału
- jeżeli zamiast sinusa wstawimy dowolną liczbę z przedziału 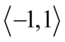 to w module otrzymamy wartości różnych znaków - nie tylko dodatnią i równą zero, ale także ujemne. Sprawdźmy więc kilka przykładowych liczb:
to w module otrzymamy wartości różnych znaków - nie tylko dodatnią i równą zero, ale także ujemne. Sprawdźmy więc kilka przykładowych liczb:
np. 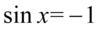 i wtedy
i wtedy  czyli
czyli 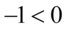
np. 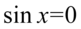 i wtedy
i wtedy  czyli
czyli 
np. 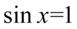 i wtedy
i wtedy  czyli
czyli 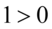
Moduł działa w następujący sposób: w przypadku liczb dodatnich i zera nie dzieje się nic, natomiast liczby ujemne są zamieniane na dodatnie przez „wybijanie” minusa z wyniku drugim minusem np.  (minus wybijający na czerwono).
(minus wybijający na czerwono).
Przy opuszczaniu modułu tam, gdzie wynik był zawsze na plusie bądź równy zero nie trzeba zmieniać znaków, tylko zamieniamy moduł na zwykły nawias, aby nie pogubić znaków przy wykonywaniu późniejszych działań (tu akurat nie ma takiego niebezpieczeństwa), natomiast w przypadku cosinusa nie możemy opuścić modułu bez dodatkowych założeń, ponieważ w zależności od liczby podstawianej za cosinus wynik jest dodatni albo ujemny (raz wybijamy minus, raz nie). Zatem wracając do tożsamości otrzymujemy:
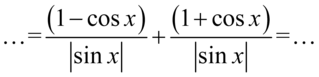
Mamy już wspólny mianownik, także można zapisać wszystko na jednej kresce ułamkowej i opuścić nawiasy w liczniku:
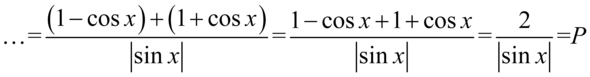
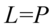
II sposób
Jest to bardziej pracochłonny sposób, ale zasada jest identyczna jak wcześniej. Zaczniemy od domnożenia tym razem liczników przez wyrażenie z przeciwnym znakiem. Oczywiście mianowniki również należy wymnożyć, ponieważ tylko wtedy wartość wyrażenia nie ulegnie zmianie. Pamiętajmy o nawiasach:
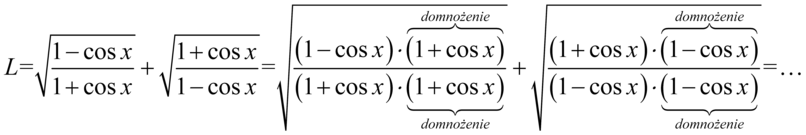
Teraz uprościmy obydwa liczniki pozbywając się nawiasów. Można to zrobić „na piechotę” kolejno wymnażając składniki lub stosując wzór skróconego mnożenia 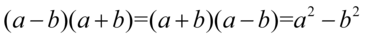 , ponieważ w obu ułamkach zawartość nawiasów różni się tylko znakiem w środku, co jest charakterystyczne dla podanego wzoru. Natomiast mianowniki zapiszemy w nieco prostszej postaci – w obu ułamkach powstały dwa identyczne nawiasy wymnożone przez siebie, a więc
, ponieważ w obu ułamkach zawartość nawiasów różni się tylko znakiem w środku, co jest charakterystyczne dla podanego wzoru. Natomiast mianowniki zapiszemy w nieco prostszej postaci – w obu ułamkach powstały dwa identyczne nawiasy wymnożone przez siebie, a więc 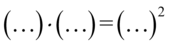 :
:
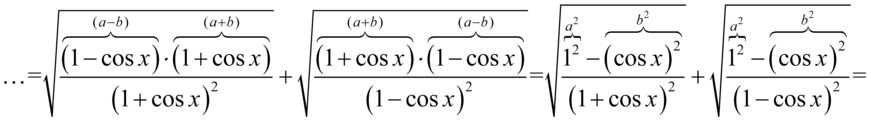
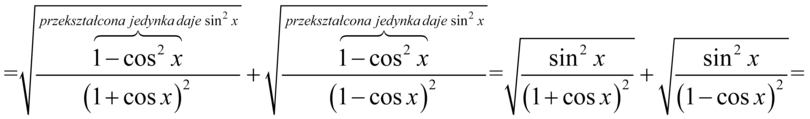
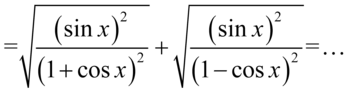
Kolejny etap stanowi likwidacja pierwiastków i tutaj niezbędna okaże się znajomość wzorów związanych z wartością bezwzględną. Na początku skorzystamy z własności działań na pierwiastkach tzn. 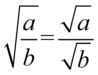 i wejdziemy z pierwiastkami w obydwu ułamkach w licznik i mianownik :
i wejdziemy z pierwiastkami w obydwu ułamkach w licznik i mianownik :
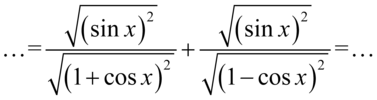
Teraz skorzystamy z własności 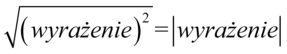 , co wyjaśnia, dlaczego nawiasy w mianownikach obydwu ułamków nie był wcześniej wymnażane tylko sprowadzone do nawiasów podniesionych do kwadratu :
, co wyjaśnia, dlaczego nawiasy w mianownikach obydwu ułamków nie był wcześniej wymnażane tylko sprowadzone do nawiasów podniesionych do kwadratu :
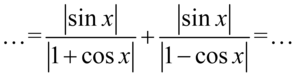
Wyjaśnienie dotyczące opuszczania modułów znajduje się w sposobie I i jest identyczne, także od razu przejdziemy do wyniku:
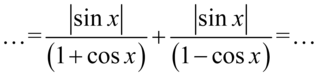
Po prawej stronie do której uzyskania dążymy mamy tylko jedną kreską ułamkową, zatem obydwa ułamki sprowadzamy do wspólnego mianownika:
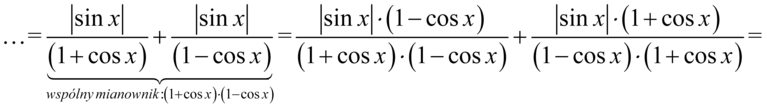
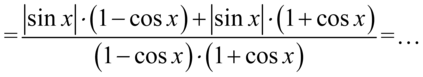
Jak widać nie ma możliwości skracania, ponieważ w liczniku jest znak dodawania, który nie jest zamknięty w nawiasie, zatem pozbędziemy się nawiasów z licznika i mianownika. W mianowniku można wymnożyć nawiasy korzystając ponownie ze wzoru skróconego mnożenia 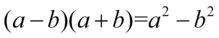 , ponieważ zawartość nawiasów różni się od siebie tylko znakiem pośrodku. Oczywiście mnożna wymnażać „na piechotę” - wynik będzie ten sam. Z kolei licznik można również wymnożyć na piechotę ( i tak zrobimy), pamiętając, że moduł zostaje bez zmian, lub wyciągnąć
, ponieważ zawartość nawiasów różni się od siebie tylko znakiem pośrodku. Oczywiście mnożna wymnażać „na piechotę” - wynik będzie ten sam. Z kolei licznik można również wymnożyć na piechotę ( i tak zrobimy), pamiętając, że moduł zostaje bez zmian, lub wyciągnąć 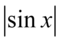 przed nawias:
przed nawias:
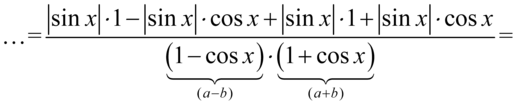
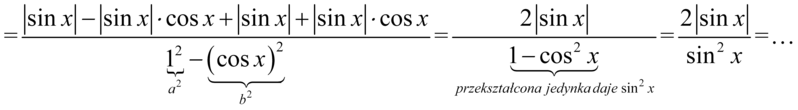
Wynik jest nieco podobny do prawej strony tożsamości, ale w liczniku mamy 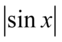 , którego należy się pozbyć. W tym momencie skorzystamy z własności, że każde wyrażenie podniesione do kwadratu można zapisać w następujący sposób
, którego należy się pozbyć. W tym momencie skorzystamy z własności, że każde wyrażenie podniesione do kwadratu można zapisać w następujący sposób 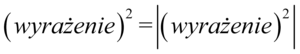 , ponieważ każde wyrażenie podniesione do kwadratu ma wartość równą zero, lub większą od zera, zatem nałożenie modułu na wynik nic nie zmieni, bo moduł w przypadku liczb dodatnich lub równych zero nic nie zmienia:
, ponieważ każde wyrażenie podniesione do kwadratu ma wartość równą zero, lub większą od zera, zatem nałożenie modułu na wynik nic nie zmieni, bo moduł w przypadku liczb dodatnich lub równych zero nic nie zmienia:
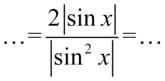
Teraz rozpiszemy kwadrat sinusa w mianowniku na iloczyn dwóch sinusów:
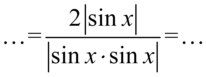
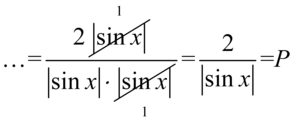
I skorzystamy z własności wartości bezwzględnej 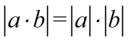 oraz skrócimy elementy z licznika i mianownika, bo między składnikami jest wyłącznie mnożenie:
oraz skrócimy elementy z licznika i mianownika, bo między składnikami jest wyłącznie mnożenie: