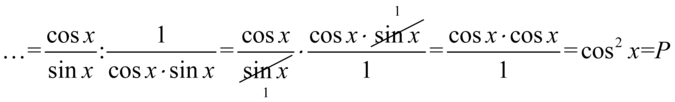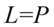Przykład 109
[kliknij aby rozwinąć] 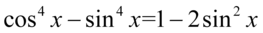
W tym przykładzie obie strony mają podobną długość, jednak po lewej stronie występują wyższe wartości potęg i to właśnie lewa strona będzie przekształcana. Trzeba się tu wykazać znajomością wzorów skróconego mnożenia. Na początku zapiszemy czwórki z wykładników potęg za pomocą dwójek, ponieważ po prawej stronie znajdują się właśnie dwójki:

Teraz skorzystamy z własności potęg, gdzie 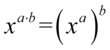 :
:
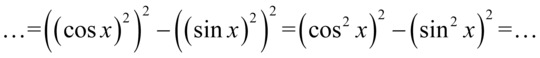
Teraz przyjrzyjmy się powstałemu wynikowi - mamy dwa elementy poniesione do kwadratu, które są oddzielone znakiem minus. I w tym momencie trzeba użyć wzoru skróconego mnożenia 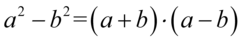 do rozłożenia powstałego wyrażenia na czynniki (czyli iloczyn nawiasów):
do rozłożenia powstałego wyrażenia na czynniki (czyli iloczyn nawiasów):
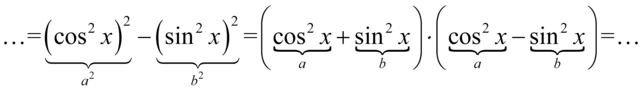
Teraz przyjrzyjmy się zawartości nawiasów, w pierwszym z nich otrzymaliśmy jedynkę trygonometryczną:
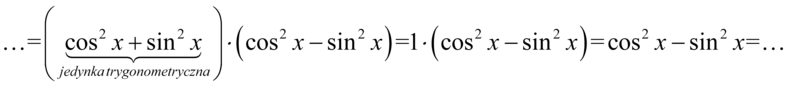
I w końcu ostatnie przekształcenie, które będzie polegało na zlikwidowaniu cosinusa, ponieważ po prawej stronie równości cosinus nie występuje. W przykładzie mamy cosinus do kwadratu, także można go ławo zamienić na sinus korzystając ze wzoru na przekształconą jedynkę trygonometryczną 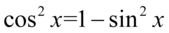 . Pamiętajmy o używaniu nawiasów, tu nie jest to koniecznie, ale lepiej użyć ich profilaktycznie aby nie pogubić znaków:
. Pamiętajmy o używaniu nawiasów, tu nie jest to koniecznie, ale lepiej użyć ich profilaktycznie aby nie pogubić znaków:
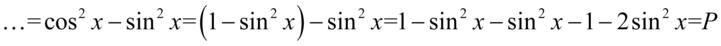
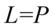
Przykład 110
[kliknij aby rozwinąć] 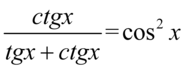
Założenie: 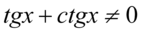 (mianownik nie może być równy
(mianownik nie może być równy  ). Po przekształceniu otrzymujemy
). Po przekształceniu otrzymujemy  .
.
Uprzedzam, że nie można stosować skracania typu 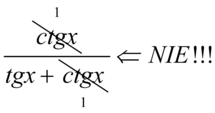 , ponieważ w mianowniku występuje dodawanie, a skracanie jest możliwe tylko wtedy, gdy dodawanie jest zamknięte w nawiasie wraz z otaczającymi je elementami
, ponieważ w mianowniku występuje dodawanie, a skracanie jest możliwe tylko wtedy, gdy dodawanie jest zamknięte w nawiasie wraz z otaczającymi je elementami 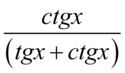 . Wnętrze nawiasu jest „święte” i nie można skracać stąd żadnego elementu, a poza nawiasem nie ma nic do skracania, (gdyby było to musi być znak mnożenia między tym elementem i nawiasem).
. Wnętrze nawiasu jest „święte” i nie można skracać stąd żadnego elementu, a poza nawiasem nie ma nic do skracania, (gdyby było to musi być znak mnożenia między tym elementem i nawiasem).
Lewa strona równości jest dłuższa, zatem to ją będziemy przekształcać, zaczniemy od skorzystania ze wzorów 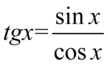 oraz
oraz 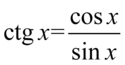 aby pozbyć się tangensa i cotangensa, ponieważ po prawej stronie występuje cosinus bez tangensów i cotangensów.
aby pozbyć się tangensa i cotangensa, ponieważ po prawej stronie występuje cosinus bez tangensów i cotangensów.
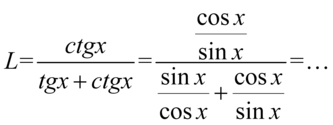
W mianowniku pierwotnego ułamka powstały dwa ułamki, które teraz sprowadzimy do wspólnego mianownika:
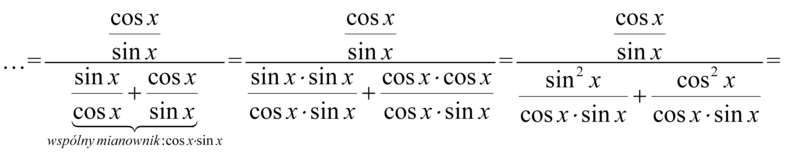
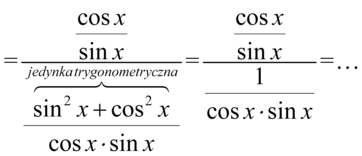
Teraz pozbędziemy się piętrowego ułamka zastępując główną kreskę ułamkową znakiem dzielenia i zamieniając dzielenie na mnożenie odwracając drugi ułamek i wykonać skracanie: