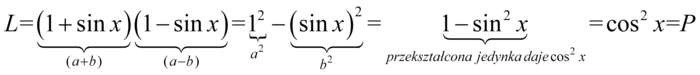Przykład 105
[kliknij aby rozwinąć] 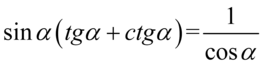
Założenie: 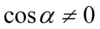 (mianownik nie może być równy
(mianownik nie może być równy  )
)
Odsyłam do przykładu 103, gdzie należy pominąć pierwsze przekształcenie, dalszy ciąg dotyczy danego przykładu.
Przykład 106
[kliknij aby rozwinąć] 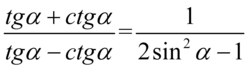
Założenie: 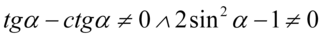 (żaden z mianowników nie może być równy
(żaden z mianowników nie może być równy  ). Przekształcając pierwszy warunek otrzymujemy
). Przekształcając pierwszy warunek otrzymujemy 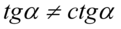 , natomiast drugi:
, natomiast drugi: 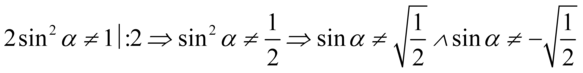
Otrzymujemy ostatecznie: 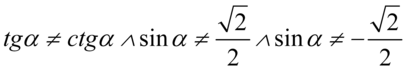
Znów przestrzegam przed błędnym skracaniem w stylu 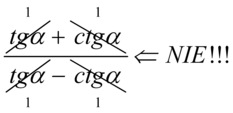 . Aby skracanie było możliwe znak dodawania lub odejmowania wraz z otaczającymi go elementami musi być zamknięty w nawiasie
. Aby skracanie było możliwe znak dodawania lub odejmowania wraz z otaczającymi go elementami musi być zamknięty w nawiasie 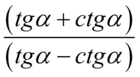 . Jak widać nie ma żadnej możliwości skracania, wnętrze nawiasu jest nietykalne. Można skracać zawartość nawiasu tylko w przypadku, gdy zawartość drugiego z nawiasów jest identyczna.
. Jak widać nie ma żadnej możliwości skracania, wnętrze nawiasu jest nietykalne. Można skracać zawartość nawiasu tylko w przypadku, gdy zawartość drugiego z nawiasów jest identyczna.
Będziemy przekształcać lewą stronę, ponieważ mamy tu tangensy i cotangensy, które łatwiej zamienić na sinusy i cosinusy niż postąpić odwrotnie. Nie ma tu żadnych charakterystycznych wzorów np. jedynki trygonometrycznej, także na początku pozbędziemy się tangensów i cotangensów korzystając ze wzorów 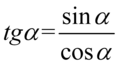 oraz
oraz 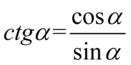 , ponieważ po prawej stronie do której uzyskania dążymy tangensy i cotangensy się występują:
, ponieważ po prawej stronie do której uzyskania dążymy tangensy i cotangensy się występują:
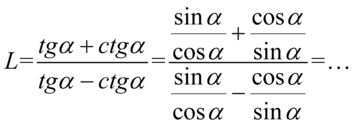
Teraz ułamki z każdego piętra sprowadzimy do wspólnego mianownika:
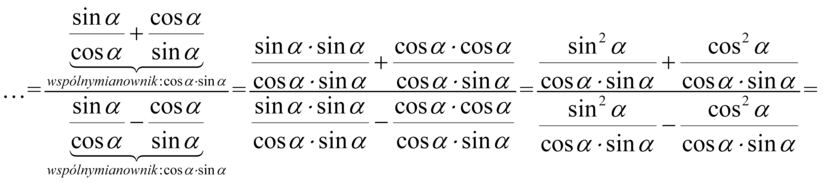
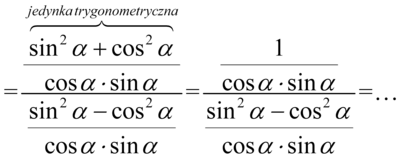
Kolejny etap to zlikwidowanie piętrowego ułamka. Główną kreskę ułamkową zastąpimy znakiem dzielenia, a następnie dzielenie zamienimy na mnożenie odwracając dzielnik czyli drugi ułamek:
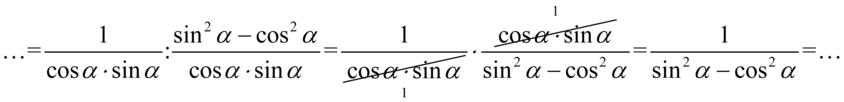
Skracanie było możliwe, ponieważ pomiędzy sinusem a cosinusem był znak mnożenia.
Wynik przypomina nieco prawą stronę, ale musimy pozbyć się cosinusa, ponieważ po prawej stronie nie występuje. Mamy komfortową sytuację, ponieważ cosinus podniesiony do kwadratu można łatwo zamienić na sinus korzystając z przekształconej jedynki trygonometrycznej 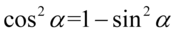 . Pamiętajmy o użyciu nawiasów, aby nie pogubić znaków:
. Pamiętajmy o użyciu nawiasów, aby nie pogubić znaków:
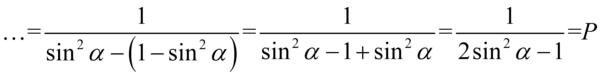
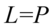
Przykład 107
[kliknij aby rozwinąć] 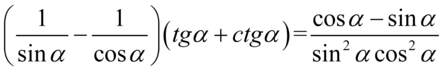
Założenie: 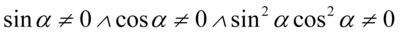 (żaden z mianowników nie może być równy
(żaden z mianowników nie może być równy  ). Rozbijając ostatni warunek otrzymujemy
). Rozbijając ostatni warunek otrzymujemy 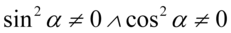 , ponieważ iloczyn dwóch składników będzie różny od zera, jeżeli każdy składnik z osobna będzie różny od zera (jeżeli pomiędzy wyrażeniami nie ma znaku to jest to kropka). Ostatecznie łącząc wszystkie warunki mamy:
, ponieważ iloczyn dwóch składników będzie różny od zera, jeżeli każdy składnik z osobna będzie różny od zera (jeżeli pomiędzy wyrażeniami nie ma znaku to jest to kropka). Ostatecznie łącząc wszystkie warunki mamy: 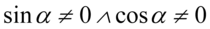 , bo składnik podniesiony do kwadratu będzie różny od zera jeżeli on sam będzie różny od zera.
, bo składnik podniesiony do kwadratu będzie różny od zera jeżeli on sam będzie różny od zera.
Ponownie przestrzegam przed skracaniem w stylu 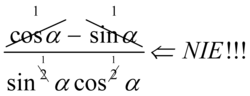 . O ile mianownik jest w idealnej formie do skracania (samo mnożenie), to jednak w liczniku występuję znak odejmowania, który wraz z otaczającymi go elementami musi być zamknięty w nawiasie. Po zamknięciu w nawiasie
. O ile mianownik jest w idealnej formie do skracania (samo mnożenie), to jednak w liczniku występuję znak odejmowania, który wraz z otaczającymi go elementami musi być zamknięty w nawiasie. Po zamknięciu w nawiasie 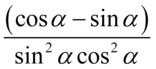 nie ma już z czym skracać mianownika, ponieważ każdy element z wnętrza nawiasu jest nietykalny. Można skracać nawias tylko jako całość.
nie ma już z czym skracać mianownika, ponieważ każdy element z wnętrza nawiasu jest nietykalny. Można skracać nawias tylko jako całość.
Lewa strona równości jest dłuższa, zatem to ona będzie podlegać przekształceniom. Na początku pozbędziemy się nawiasów wymnażając kolejno składniki:
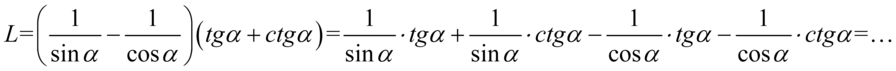
Nie mamy tu żadnych charakterystycznych wzorów, także kolejnym krokiem jest zamiana tangensa i cotangensa ze wzorów 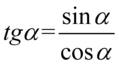 oraz
oraz 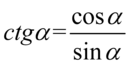 , ponieważ po prawej stronie nie występują:
, ponieważ po prawej stronie nie występują:
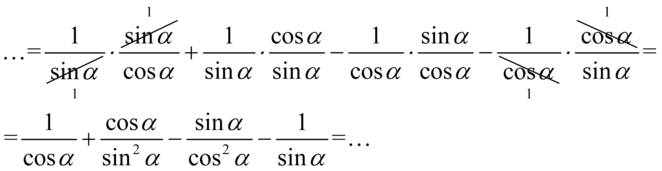
Powstały cztery ułamki, a po prawej stronie mamy jedną kreskę ułamkową, także kolejny krok sprowadzenie ułamków do wspólnego mianownika. W tym przypadku postarajmy się o najmniejszy wspólny mianownik. Oddzielenie sprowadzimy do wspólnego mianownika ułamki z sinusem na dole oraz oddzielnie z cosinusem na dole, ponieważ sprowadzenie do wspólnego mianownika wszystkich ułamków jednocześnie znacznie skomplikuje licznik w nowo powstałym ułamku, a dalsze przekształcenia będę znacznie trudniejsze do wykonania. Oczywiście można znaleźć jeden wspólny mianownik dla wszystkich. Tworząc wspólny mianownik trzeba przyjrzeć się każdemu mianownikowi - i tak mamy  oraz
oraz  , gdzie
, gdzie 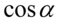 zawiera się w
zawiera się w 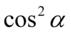 , bo
, bo 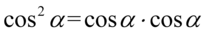 , analogicznie z sinusem -
, analogicznie z sinusem - 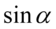 zawiera się w
zawiera się w 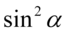 , bo
, bo  . Na początku zmienię kolejność ułamków, tak aby ułamki z sinusem na dole znajdowały się obok siebie, podobnie z cosinusami na dole:
. Na początku zmienię kolejność ułamków, tak aby ułamki z sinusem na dole znajdowały się obok siebie, podobnie z cosinusami na dole:
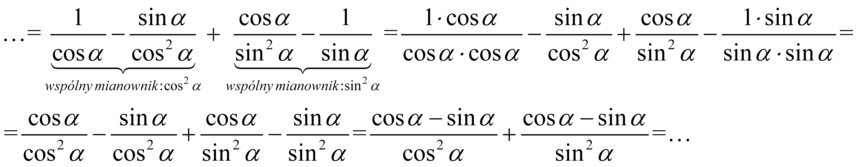
Powstałe ułamki ponownie sprowadzimy do wspólnego mianownika:
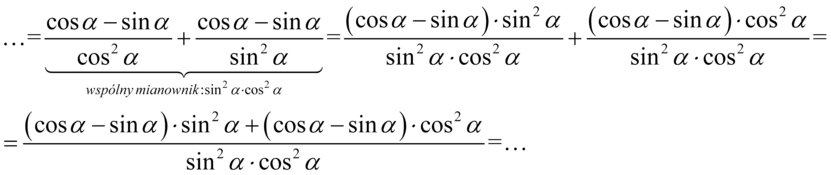
Teraz można pozbyć się nawiasów, ale ich zawartość jest zgodna z tym co chcemy otrzymać, a więc z licznikiem ułamka z prawej strony. W związku z tym wyciągniemy powtarzający się nawias jako wspólny czynnik, a w drugim nawiasie wpisujemy elementy, które zostały po zabraniu pierwszego nawiasu:
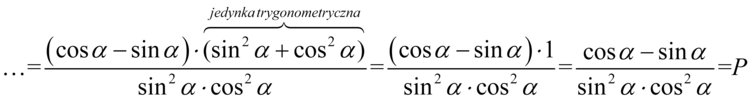
Przykład 108
[kliknij aby rozwinąć] 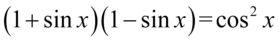
Lewa strona tożsamości jest dłuższa, zatem to ona będzie podlegać przekształceniom. Na początku pozbędziemy się nawiasów. Można to zrobić dwojako - mnożąc kolejno wszystkie składniki lub zauważyć, że zawartość tychże nawiasów różni się od siebie tylko znakiem w środku, a więc możliwe jest zastosowanie wzoru skróconego mnożenia 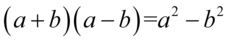 . Ja zastosuję ten drugi sposób, ale też można wymnożyć „na piechotę”, a i tak wynik będzie ten sam:
. Ja zastosuję ten drugi sposób, ale też można wymnożyć „na piechotę”, a i tak wynik będzie ten sam: