
Przykład 101
[kliknij aby rozwinąć] 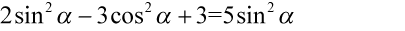
Lewa strona równości jest dłuższa, zatem to ona będzie podlegać przekształceniom. Po prawej stronie, którą chcemy uzyskać jest tylko sinus, tak więc musimy pozbyć się cosinusa. Cosinus podniesiony jest do kwadratu, więc możemy wykorzystać tu przekształconą jedynkę trygonometryczną 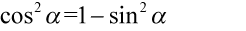 przy zamianie. Pamiętajmy o nawiasach aby nie pogubić znaków:
przy zamianie. Pamiętajmy o nawiasach aby nie pogubić znaków:
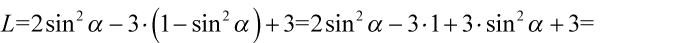
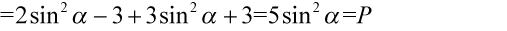
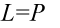
Przykład 102
[kliknij aby rozwinąć] 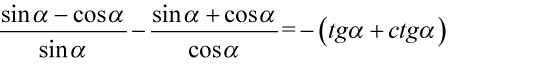
Założenie: 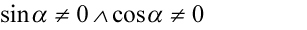 (żaden mianownik nie może być równy
(żaden mianownik nie może być równy 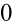 )
)
Daną tożsamość można udowodnić na dwa sposoby – mniej i bardziej pracochłonny. W obu przypadkach będziemy zajmować się lewą stroną, ponieważ jest dłuższa.
I sposób
Rozdzielimy obydwa ułamki na dwa mniejsze, analogicznie jak wykonuje się to na prostych liczbach np. 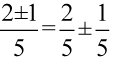 . Pamiętajmy, że drugi ułamek po rozdzieleniu należy zapisać w nawiasie, ponieważ stoi przed nim minus i istnieje niebezpieczeństwo, że pogubimy znaki:
. Pamiętajmy, że drugi ułamek po rozdzieleniu należy zapisać w nawiasie, ponieważ stoi przed nim minus i istnieje niebezpieczeństwo, że pogubimy znaki:
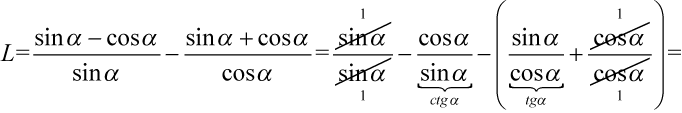
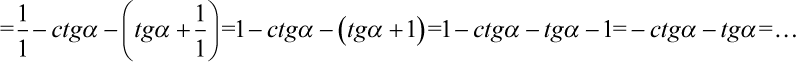
Mamy jeszcze utworzyć nawias poprzez wyciągnięcie minusa i zmienimy kolejność w nawiasie. Przy dodawaniu nie zmienia to wyniku:
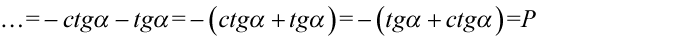
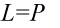
II sposób
Sprowadzimy obydwa ułamki do wspólnego mianownika:
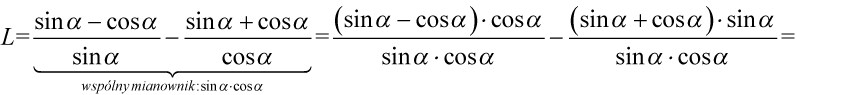
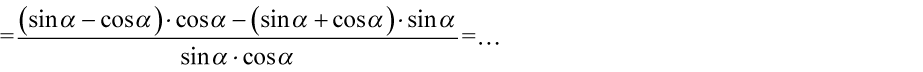
Teraz pozbędziemy się nawiasów w liczniku wymnażając odpowiednio składniki:
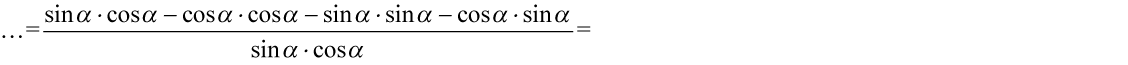
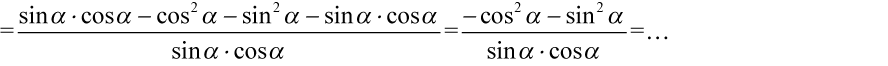
Teraz musimy uzyskać dwa elementy jak po prawej stronie poprzez rozdzielenie ułamka na dwa analogicznie jak się to wykonuje na prostszych ułamkach np. 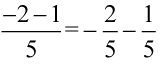 :
:
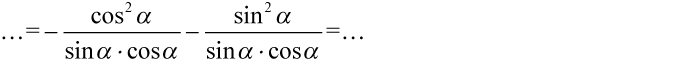
W każdym ułamku pomiędzy składnikami w mianowniku i liczniku występuje wyłącznie znak mnożenia, także można skracać bez obaw:
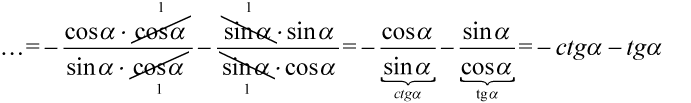
Mamy jeszcze utworzyć nawias poprzez wyciągnięcie minusa i zmienimy kolejność w nawiasie. Przy dodawaniu nie zmienia to wyniku:
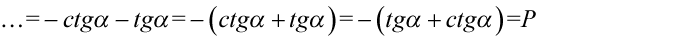
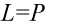
Przykład 103
[kliknij aby rozwinąć] 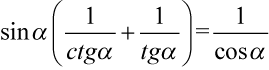
Założenie: 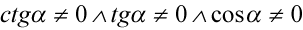 (żaden mianownik nie może być równy
(żaden mianownik nie może być równy 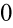 )
)
Lewa strona tożsamości jest dłuższa, zatem to ona będzie podlegać przekształceniom. Na początku warto przyjrzeć się zawartości nawiasów. Mamy tu dwa wzory, które pozwolą nieco uprościć zawartość nawiasów 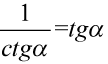 oraz
oraz 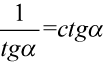 :
:
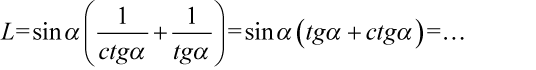
Teraz pozbędziemy się nawiasów kolejno wymnażając składniki:
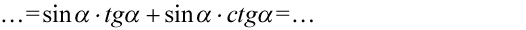
Po prawej stronie, którą chcemy uzyskać nie ma tangensów i cotangensów, także zamienimy je na sinusy i cosinusy ze wzorów: 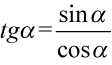 oraz
oraz 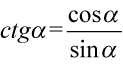 :
:
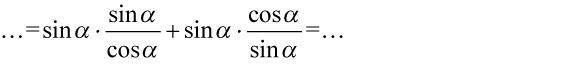
Dla ułatwienia działań zastosujemy zapis 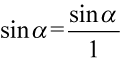 oraz
oraz 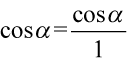 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez 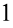 nie ulega zmianie, a dzięki temu zapisowi będzie wiadomo co wymnażamy, a co skracamy:
nie ulega zmianie, a dzięki temu zapisowi będzie wiadomo co wymnażamy, a co skracamy:
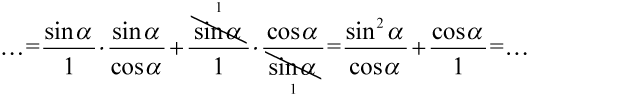
Teraz sprowadzimy obydwa ułamki do wspólnego mianownika, ponieważ po prawej stronie mamy jeden ułamek:
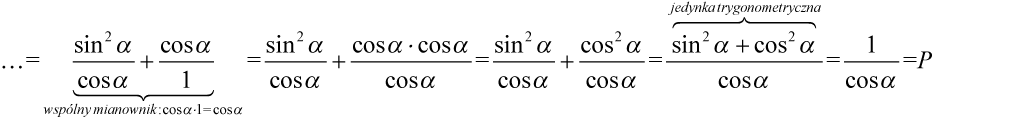
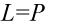
Przykład 104
[kliknij aby rozwinąć] 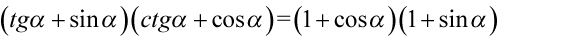
Obie strony równości mają podobną długość, ale po lewej stronie w nawiasach mamy tangensy i cotangensy, które łatwiej zamienić na sinusy i cosinusy, niż z jedynek utworzyć tangensy i cotangensy.
Na początku pozbędziemy się nawiasów wymnażając kolejno składniki:
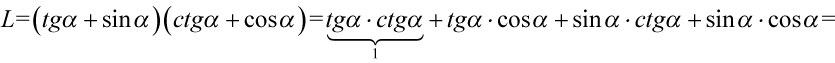
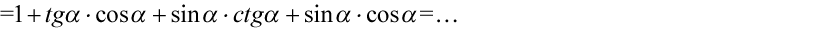
Teraz pozbędziemy się tangensów i cotangensów, ponieważ po prawej stronie ich nie ma. Skorzystamy ze wzorów 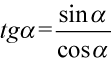 i
i 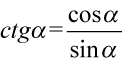 :
:
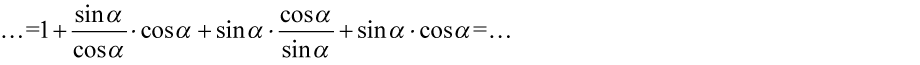
Dla ułatwienia działań zastosujemy zapis 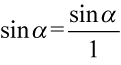 oraz
oraz 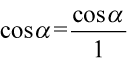 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez 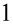 nie ulega zmianie, a dzięki temu zapisowi będzie wiadomo co wymnażamy, a co skracamy:
nie ulega zmianie, a dzięki temu zapisowi będzie wiadomo co wymnażamy, a co skracamy:
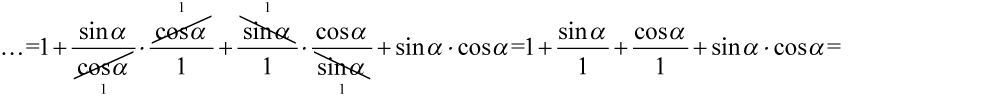
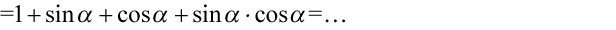
Teraz najtrudniejszy etap, musimy znów utworzyć nawiasy. W tym celu pogrupujemy w nawiasy po dwa składniki co nie zmieni wyniku:
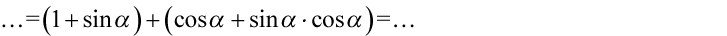
Następnie wyłączamy wspólny czynnik przed nawias o ile to możliwe, w drugim nawiasie powtarza się 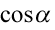 - czyli to stanowi wspólny czynnik. Pamiętamy, że po zabraniu „wszystkiego” zostaje
- czyli to stanowi wspólny czynnik. Pamiętamy, że po zabraniu „wszystkiego” zostaje 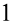 . W pierwszym nawiasie nie ma elementu powtarzającego się, w takim przypadku wyciągajmy
. W pierwszym nawiasie nie ma elementu powtarzającego się, w takim przypadku wyciągajmy 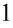 przed nawias, nie jest to konieczne, ale znacznie ułatwia dalsze działania:
przed nawias, nie jest to konieczne, ale znacznie ułatwia dalsze działania:
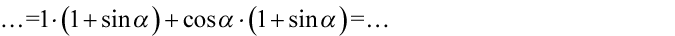
Jak widać powstały identyczne nawiasy, w tym momencie to 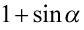 staje się wspólnym czynnikiem, który znów wyciągamy tworząc kolejny nawias. Inaczej mówiąc przepisujemy powtarzający się nawias, a w drugim nawiasie wpisujemy „sieroty” :) z wszystkimi znakami, które zostały po zabraniu tego nawiasu:
staje się wspólnym czynnikiem, który znów wyciągamy tworząc kolejny nawias. Inaczej mówiąc przepisujemy powtarzający się nawias, a w drugim nawiasie wpisujemy „sieroty” :) z wszystkimi znakami, które zostały po zabraniu tego nawiasu:
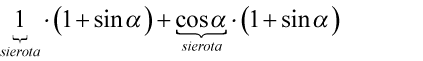
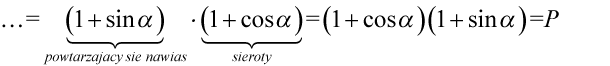
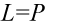
Na końcu zmieniono kolejność nawiasów aby uzyskać prawą stronę identyczną jak w wyjściowym przykładzie, pomiędzy nawiasami jest znak mnożenia, a jak wiadomo mnożenie jest przemienne.