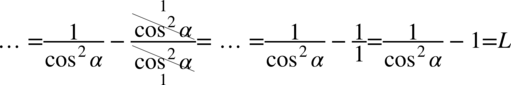Przykład 97
[kliknij aby rozwinąć] 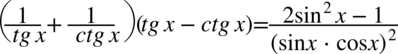
Założenie: 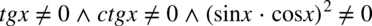 (żaden mianownik nie może być równy
(żaden mianownik nie może być równy  ). Ostatecznie otrzymujemy
). Ostatecznie otrzymujemy 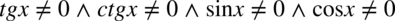 , ponieważ iloczyn dwóch składników jest różny od zera, a tym bardziej kwadrat iloczynu, gdy każdy ze składników z osobna jest różny od zera.
, ponieważ iloczyn dwóch składników jest różny od zera, a tym bardziej kwadrat iloczynu, gdy każdy ze składników z osobna jest różny od zera.
Od razu przestrzegam przed błędnym skracaniem w stylu  , ponieważ w liczniku ułamka występuje znak odejmowania, który wraz z otaczającymi elementami nie jest zamknięty w nawiasie. Po zamknięciu odejmowania w nawiasie
, ponieważ w liczniku ułamka występuje znak odejmowania, który wraz z otaczającymi elementami nie jest zamknięty w nawiasie. Po zamknięciu odejmowania w nawiasie 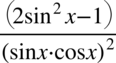 nie ma już możliwości skracania, ponieważ wnętrze nawiasu można skracać tylko z identycznym wnętrzem innego nawiasu.
nie ma już możliwości skracania, ponieważ wnętrze nawiasu można skracać tylko z identycznym wnętrzem innego nawiasu.
Lewa strona tożsamości jest dłuższa, zatem to ona będzie przekształcana. Na początku przyjrzyjmy się zawartości pierwszego nawiasu, gdzie występują elementy, które można krócej zapisać korzystając ze wzorów 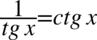 oraz
oraz  :
:
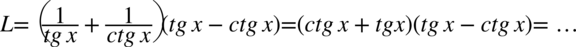
Teraz pozbędziemy się nawiasów, ponieważ po prawej stronie, do której uzyskania dążymy nie występują. Można to zrobić wymnażając kolejno składniki albo skorzystać ze wzoru skróconego mnożenia 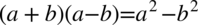 po zmianie kolejności składników w pierwszym nawiasie (w dodawaniu nie zmienia to wyniku), bo wtedy nawiasy będą różnić się tylko znakiem w środku:
po zmianie kolejności składników w pierwszym nawiasie (w dodawaniu nie zmienia to wyniku), bo wtedy nawiasy będą różnić się tylko znakiem w środku:
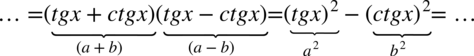
Kolejny krok to zamiana tangensa i cotangensa ze wzorów 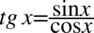 oraz
oraz 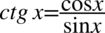 , ponieważ po prawej stronie nie ma tangensa ani cotangensa:
, ponieważ po prawej stronie nie ma tangensa ani cotangensa:
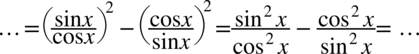
Teraz powstałe ułamki sprowadzimy do wspólnego mianownika – dzięki temu uzyskamy jeden ułamek:
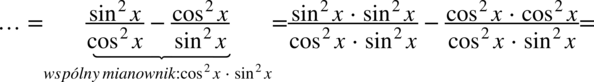
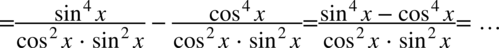
Właściwie mianownik powstałego ułamka jest bardzo zbliżony do pożądanego wyniku, wystarczy zmienić kolejność składników w mnożeniu i skorzystać z własności potęg 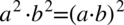 :
:
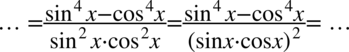
Teraz musimy zając się licznikiem, gdzie występują wykładniki wyższego stopnia niż po prawej. Trzeba się tu wykazać znajomością wzorów skróconego mnożenia. Na początku zapiszemy czwórki z wykładników potęg za pomocą dwójek, ponieważ po prawej stronie znajdują się właśnie dwójki:

Teraz skorzystamy z własności potęg, gdzie  :
:

Na tym etapie przyjrzyjmy się powstałemu wynikowi - mamy dwa elementy poniesione do kwadratu, które są oddzielone znakiem minus. I w tym momencie trzeba użyć wzoru skróconego mnożenia 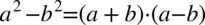 do rozłożenia powstałego wyrażenia na czynniki (czyli iloczyn nawiasów):
do rozłożenia powstałego wyrażenia na czynniki (czyli iloczyn nawiasów):
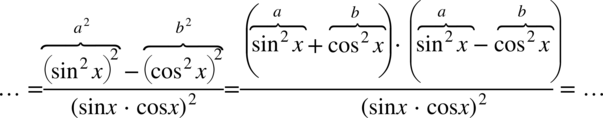
Teraz przyjrzyjmy się zawartości nawiasów, w pierwszym z nich otrzymaliśmy jedynkę trygonometryczną:
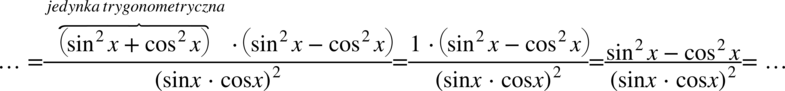
W liczniku po prawej stronie występują wyłącznie sinusy, a dysponujemy cosinusem do kwadratu, który łatwo zamienić na sinus korzystając ze wzoru na przekształconą jedynkę trygonometryczną 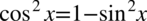 . Nie zapominajmy o nawiasach aby nie pogubić znaków:
. Nie zapominajmy o nawiasach aby nie pogubić znaków:
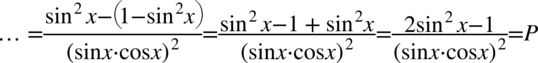

Przykład 98
[kliknij aby rozwinąć] 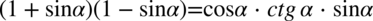
Obie strony są podobnej długości, ale po prawej mamy cotangens, który znacznie łatwiej zamienić na sinus i cosinus niż stworzyć z jedynek i sinusów cotangens. Tak więc pierwszym krokiem będzie likwidacja cotangensa przy użyciu wzoru 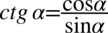 :
:
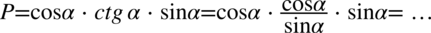
Aby ułatwić dalsze działania zostanie użyty zapis 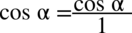 oraz
oraz 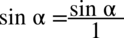 (każda liczba lub wyrażenie podzielone przez
(każda liczba lub wyrażenie podzielone przez  nie ulega zmianie). Dzięki temu wiadomo, które elementy można skracać:
nie ulega zmianie). Dzięki temu wiadomo, które elementy można skracać:

Przyglądając się lewej stronie widzimy tam jedynki i sinusy, otrzymaliśmy cosinus podniesiony do kwadratu, który można z łatwością zamienić na sinus korzystając ze wzoru na przekształconą jedynkę trygonometryczną 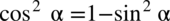 :
:
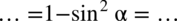
Teraz musimy stworzyć nawiasy. Warto zauważyć, że w wyniku mamy dwa elementy oddzielone minusem, w tym jeden podniesiony do kwadratu, co jest charakterystyczne dla wzoru skróconego mnożenia postaci: 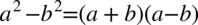 . Aby łatwiej go zauważyć można inaczej zapisać jedynkę
. Aby łatwiej go zauważyć można inaczej zapisać jedynkę  , bo jedynka podniesiona do dowolnej potęgi i tak wynosi
, bo jedynka podniesiona do dowolnej potęgi i tak wynosi  . Jak wyłowić
. Jak wyłowić 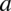 i
i 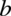 ze wzoru? Należy się zastanowić co trzeba podnieść do kwadratu aby otrzymać te dwa elementy, czyli
ze wzoru? Należy się zastanowić co trzeba podnieść do kwadratu aby otrzymać te dwa elementy, czyli  i
i 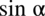 :
:
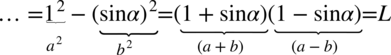

Przykład 99
[kliknij aby rozwinąć] 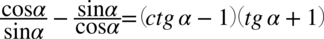
Założenie: 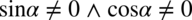 (żaden mianownik nie może być równy
(żaden mianownik nie może być równy  )
)
Po prawej stronie występują cotangens, tangens oraz nawiasy, zatem to ona będzie przekształcana, bo tą „mieszankę” łatwiej rozpisać niż do niej dojść jako wyniku. Na początku pozbędziemy się nawiasów wymnażając kolejno składniki:
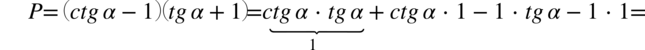
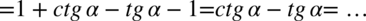
Ostatni etap to zamiana cotangensa i tangensa ze wzorów 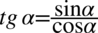 oraz
oraz 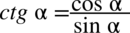 :
:
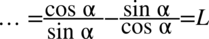

Przykład 100
[kliknij aby rozwinąć] 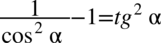
Założenie: 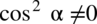 (mianownik nie może być równy
(mianownik nie może być równy  ). Po przekształceniu założenia otrzymujemy
). Po przekształceniu założenia otrzymujemy 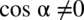 , ponieważ jeżeli cosinus jest różny od zera, to podniesiony do kwadratu także jest różny od zera.
, ponieważ jeżeli cosinus jest różny od zera, to podniesiony do kwadratu także jest różny od zera.
Powyższą tożsamość można udowodnić na dwa sposoby.
I sposób
Zaczniemy od lewej strony, gdzie występują dwa elementy: ułamek i jedynka. Po prawej stronie do której uzyskania dążymy jest tylko jeden element, w związku z tym należy z dwóch elementów stworzyć jeden sprowadzając je do wspólnego mianownika. Dla ułatwienia działań zostanie użyty zapis: 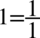 (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie):
nie ulega zmianie):
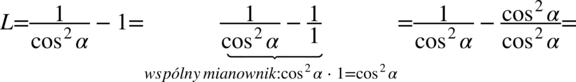

Na zakończenie zastosujemy prawa działań na potęgach 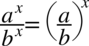 , gdzie naszym
, gdzie naszym  jest dwójka:
jest dwójka:
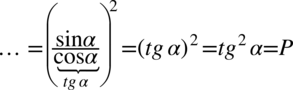

II sposób
Będziemy przekształcać prawą stronę. Po lewej stronie do której uzyskania dążymy jest cosinus i jedynka, także pierwszym krokiem będzie zamiana tangensa na sinus i cosinus zgodnie ze wzorem 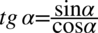 :
:

Mianownik przypomina nieco lewą stronę, a sinus podniesiony do kwadratu w liczniku można zamienić na cosinus ze wzoru na przekształconą jedynkę trygonometryczną 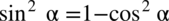 :
:
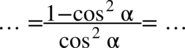
Mamy jeden ułamek, a po lewej stronie są dwa elementy. Aby je uzyskać rozpiszemy ułamek na dwa analogicznie jak wykonuje się to na ułamkach zwykłych np. 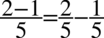 :
: