Przykład 93
[kliknij aby rozwinąć] 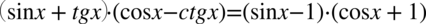
Obie strony są podobnej długości, ale po lewej stronie w nawiasach występuje tangens oraz cotangens, także to lewa strona będzie przekształcana. Na początku pozbędziemy się nawiasów wymnażając kolejno składniki:
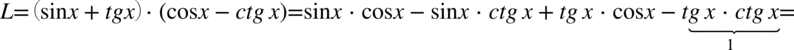
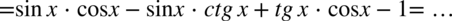
Kolejny krok to likwidacja tangensów i cotangensów ze wzorów 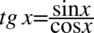 oraz
oraz 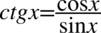 , ponieważ po prawej stronie do której uzyskania dążymy tangensy i cotangensy nie występują:
, ponieważ po prawej stronie do której uzyskania dążymy tangensy i cotangensy nie występują:
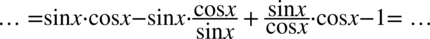
W celu ułatwienia mnożenia zostanie użyty zapis 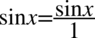 oraz
oraz 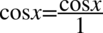 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez  nie ulega zmianie:
nie ulega zmianie:
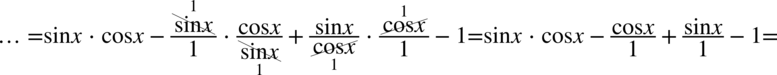
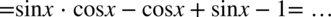
Teraz najtrudniejszy etap, musimy znów utworzyć nawiasy. W tym celu pogrupujemy w nawiasy po dwa składniki:
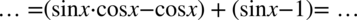
Następnie wyłączamy wspólny czynnik przed nawias o ile to możliwe, w pierwszym nawiasie powtarza się  - czyli to stanowi wspólny czynnik. Pamiętamy, że po zabraniu „wszystkiego” zostaje
- czyli to stanowi wspólny czynnik. Pamiętamy, że po zabraniu „wszystkiego” zostaje  . W drugim nawiasie nie ma nic powtarzającego się, w takim przypadku wyciągajmy
. W drugim nawiasie nie ma nic powtarzającego się, w takim przypadku wyciągajmy  przed nawias, nie jest to konieczne, ale znacznie ułatwia dalsze działania:
przed nawias, nie jest to konieczne, ale znacznie ułatwia dalsze działania:
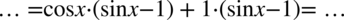
Jak widać powstał identyczne nawiasy, w tym momencie to 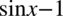 staje się wspólnym czynnikiem, który znów wyciągamy tworząc kolejny nawias. Inaczej mówiąc przepisujemy powtarzający się nawias, a w drugim nawiasie wpisujemy „sieroty” :) z wszystkimi znakami, które zostały po zabraniu tego nawiasu:
staje się wspólnym czynnikiem, który znów wyciągamy tworząc kolejny nawias. Inaczej mówiąc przepisujemy powtarzający się nawias, a w drugim nawiasie wpisujemy „sieroty” :) z wszystkimi znakami, które zostały po zabraniu tego nawiasu:
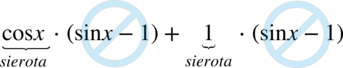


Przykład 94
[kliknij aby rozwinąć] 
Założenie: 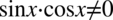 (mianownik nie może być równy
(mianownik nie może być równy  ). Aby iloczyn dwóch składników był różny od zera, każdy składnik z osobna musi być różny od zera, zatem ostatecznie:
). Aby iloczyn dwóch składników był różny od zera, każdy składnik z osobna musi być różny od zera, zatem ostatecznie: 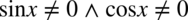
Na wstępie przestrzegam przed skracaniem 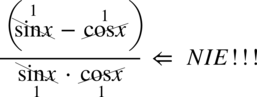 . O ile mianownik ułamka jest w idealnej formie pozwalającej na skracanie (znak mnożenia między składnikami), to jednak w liczniku występuje znak odejmowania, który je uniemożliwia. Aby skracanie było prawidłowe minus wraz z otaczającymi go składnikami musi być zamknięty w nawiasie i tu jest on zamknięty. Po nałożeniu nawiasów nie ma już z czym skrócić cosinusa i sinusa z mianownika (wnętrze nawiasu jest nietykalne, skracać można tylko nawias jako całość).
. O ile mianownik ułamka jest w idealnej formie pozwalającej na skracanie (znak mnożenia między składnikami), to jednak w liczniku występuje znak odejmowania, który je uniemożliwia. Aby skracanie było prawidłowe minus wraz z otaczającymi go składnikami musi być zamknięty w nawiasie i tu jest on zamknięty. Po nałożeniu nawiasów nie ma już z czym skrócić cosinusa i sinusa z mianownika (wnętrze nawiasu jest nietykalne, skracać można tylko nawias jako całość).
Będziemy zajmować się lewą stroną, co prawda jest ona krótsza, ale mamy tu tangens i cotangens, które znacznie łatwiej rozłożyć na sinusy i cosinusy niż działać w przeciwnym kierunku, zwłaszcza, że po utworzeniu tangensów trzeba nałożyć na nie nawiasy, co już nie jest takie proste (jeżeli chcemy przekształcać prawą w lewą stronę).
Na początku pozbędziemy się nawiasów wymnażając kolejno składniki:
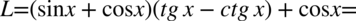
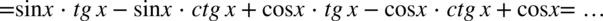
Teraz pozbędziemy się tangensów i cotangensów korzystając ze wzorów 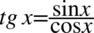 oraz
oraz 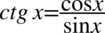 , ponieważ po prawej stronie do której uzyskania dążymy tangensy i cotangensy nie występują:
, ponieważ po prawej stronie do której uzyskania dążymy tangensy i cotangensy nie występują:
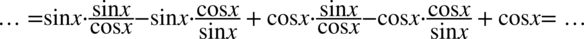
W celu ułatwienia mnożenia i skracania zostanie użyty zapis 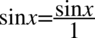 oraz
oraz 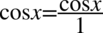 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez  nie ulega zmianie:
nie ulega zmianie:
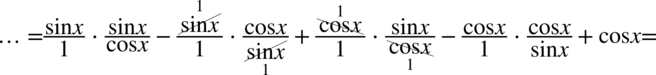

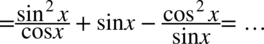
Teraz 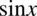 powędruje na koniec przykładu zgodnie z tym co widzimy po prawej stronie (tylko zmiana kolejności), a pozostałe dwa ułamki sprowadzimy do wspólnego mianownika:
powędruje na koniec przykładu zgodnie z tym co widzimy po prawej stronie (tylko zmiana kolejności), a pozostałe dwa ułamki sprowadzimy do wspólnego mianownika:
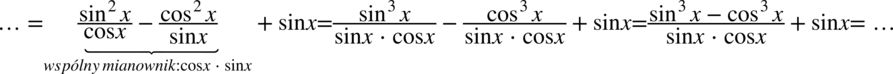
Aby otrzymać prawą stronę musimy jeszcze rozłożyć licznik ułamka na czynniki, mamy tu komfortową sytuację, ponieważ można tu skorzystać ze wzoru skróconego mnożenia 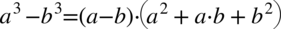 :
:

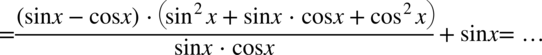
W drugim nawiasie powstał sinus i cosinus podniesiony do kwadratu, jeżeli zmienimy kolejność składników i „przytulimy” je do siebie to otrzymamy jedynkę trygonometryczną:
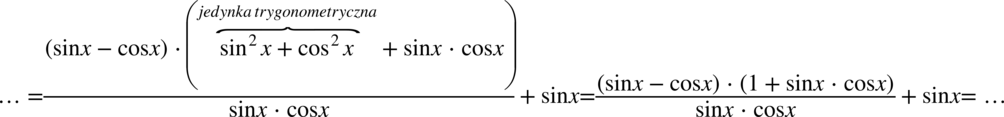
Aby uzyskać identyczny zapis wyniku występujący po prawej stronie należy „zrzucić” drugi nawias z kreski ułamkowej czyli po prostu rozdzielić mnożenie, jest to jak najbardziej prawidłowa czynność, chociaż rzadko wykonywana:
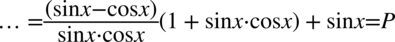

Przykład 95
[kliknij aby rozwinąć] 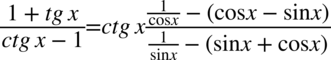
Założenie: 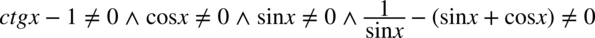
(żaden mianownik nie może być równy  )
)
Mamy: 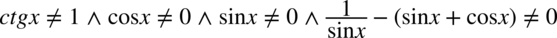
(nie rozpisujemy ostatniego warunku, ponieważ wymagałoby to rozwiązania równania trygonometrycznego, co nie jest wymagane)
Tu również przestrzegam przed błędnym skracaniem 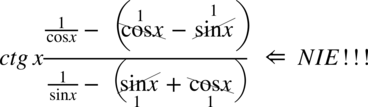 , wnętrza nawiasów nie wolno ruszać, możliwe jest tylko skracanie całości nawiasów (o ile są identyczne) i jeżeli przed nawiasem oraz poprzedzającym go składnikiem stoi znak mnożenia.
, wnętrza nawiasów nie wolno ruszać, możliwe jest tylko skracanie całości nawiasów (o ile są identyczne) i jeżeli przed nawiasem oraz poprzedzającym go składnikiem stoi znak mnożenia.
Zajmiemy się prawą stroną, która jest znacznie dłuższa od lewej. Na początku pozbędziemy się nawiasów zmieniając znaki na przeciwne:
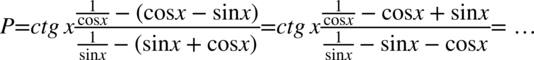
Teraz w liczniku i mianowniku „mega” ułamka zapiszemy wszystkie elementy na jednej kresce ułamkowej poprzez sprowadzenie do wspólnego mianownika. Dla ułatwienia działań zostanie użyty zapis 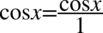 oraz
oraz 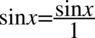 :
:
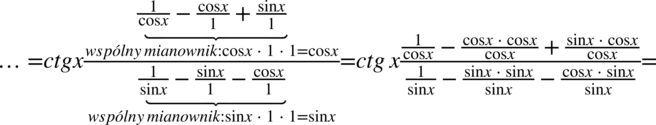

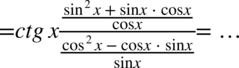
Teraz pozbędziemy się kreski ułamkowej zastępując ją znakiem dzielenia, a dzielenie ułamków zamienimy na mnożenie odwracając jednocześnie drugi ułamek:

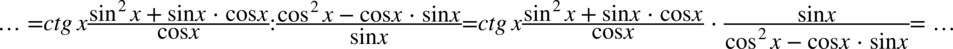
W tym momencie nie mamy możliwości skracania, ale możemy zlikwidować cotangens korzystając ze wzoru 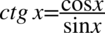 , jest on wymnożony, także skracanie jest możliwe:
, jest on wymnożony, także skracanie jest możliwe:
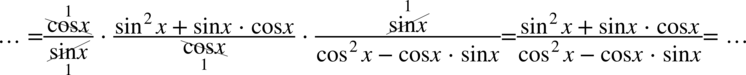
Po lewej stronie do której uzyskania dążymy występuje tangens i cotangens oraz jedynki. Właśnie te jedynki pomogą uzyskać nam pożądany wynik. Na początku wyciągnijmy przed nawias powtarzające się elementy z licznika i mianownika - w liczniku 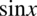 , a w mianowniku
, a w mianowniku  :
:
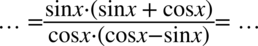
Teraz musimy uzyskać jedynki, w liczniku w nawiasie jest plus, także jedynkę można uzyskać wyciągając jeszcze raz 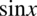 lub
lub  , bo dodawanie jest przemienne, tzn. możemy dowolnie zmienić kolejność składników, a wynik i tak nie ulegnie zmianie. Natomiast w mianowniku jedynka stoi za minusem także tu już na pewno wiadomo, że należy wyciągnąć
, bo dodawanie jest przemienne, tzn. możemy dowolnie zmienić kolejność składników, a wynik i tak nie ulegnie zmianie. Natomiast w mianowniku jedynka stoi za minusem także tu już na pewno wiadomo, że należy wyciągnąć 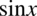 przed nawias, bo odejmowanie w przeciwieństwie do odejmowania nie jest przemienne. Jeżeli wyciągamy przed nawias element, który się nie powtarza, to najlepiej stosować zapis z kreską ułamkową, ponieważ wyciąganie wspólnego czynnika przed nawias to nic innego jak dzielenie wszystkich elementów z nawiasu przez ten wyłączony. Oczywiście pamiętamy, że jeśli wyciągamy „wszystko” z danego miejsca to zostaje
przed nawias, bo odejmowanie w przeciwieństwie do odejmowania nie jest przemienne. Jeżeli wyciągamy przed nawias element, który się nie powtarza, to najlepiej stosować zapis z kreską ułamkową, ponieważ wyciąganie wspólnego czynnika przed nawias to nic innego jak dzielenie wszystkich elementów z nawiasu przez ten wyłączony. Oczywiście pamiętamy, że jeśli wyciągamy „wszystko” z danego miejsca to zostaje  (w końcu dzielimy dany element przez siebie co zawsze daje
(w końcu dzielimy dany element przez siebie co zawsze daje  , w tym przypadku przez
, w tym przypadku przez 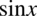 ):
):
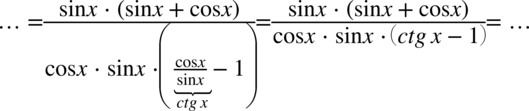
Mianownik jest już prawie satysfakcjonujący, ale przeszkadza nam 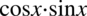 , aby się pozbyć całości tego „balastu”, należy w liczniku wyciągnąć
, aby się pozbyć całości tego „balastu”, należy w liczniku wyciągnąć  przed nawias. Dzięki temu uzyskamy też niezbędną jedynkę w liczniku:
przed nawias. Dzięki temu uzyskamy też niezbędną jedynkę w liczniku:

Dodawanie i odejmowanie wraz z otaczającymi elementami jest zamknięte w nawiasie, a pomiędzy nawiasem a sinusem i cosinusem jest znak mnożenia, także można bez obaw skracać:
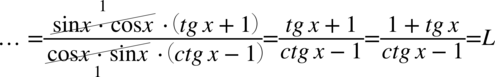

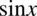
Przykład 96
[kliknij aby rozwinąć] 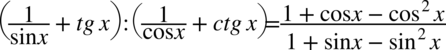
Założenie: 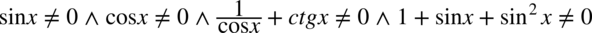
Żaden z mianowników nie może być równy  , natomiast trzecie założenie oznacza, że nie można dzielić przez
, natomiast trzecie założenie oznacza, że nie można dzielić przez  . Nie będziemy rozpisywać dwóch ostatnich założeń, ponieważ wymagają one rozwiązania równań trygonometrycznych.
. Nie będziemy rozpisywać dwóch ostatnich założeń, ponieważ wymagają one rozwiązania równań trygonometrycznych.
Lewa strona równości jest dłuższa, zatem to ona będzie przekształcana. Na początku znak dzielenia zostanie zastąpiony kreską ułamkową, co prawda powstanie piętrowy ułamek, ale w ogólnym rozrachunku będzie przejrzyściej. Przy zapisaniu na kresce ułamkowej nie trzeba już używać nawiasów:
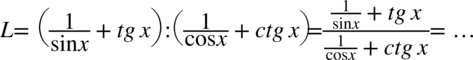
Teraz pozbędziemy się tangensa i cotangensa korzystając ze wzorów 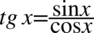 oraz
oraz 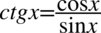 , ponieważ po prawej stronie do której uzyskania dążymy nie ma ani tangensa ani cotangensa:
, ponieważ po prawej stronie do której uzyskania dążymy nie ma ani tangensa ani cotangensa:
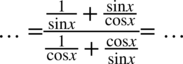
Kolejny krok to sprowadzenie do wspólnego mianownika ułamków z każdego piętra:
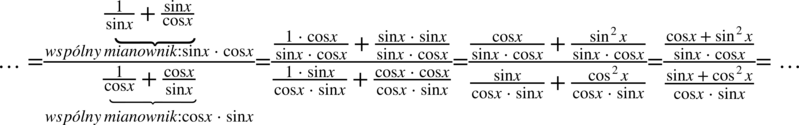
Teraz pozbędziemy się głównej kreski ułamkowej wracając do znaku dzielenia, a następnie dzielenie zamienimy na mnożenie przed odwrotność drugiego ułamka:
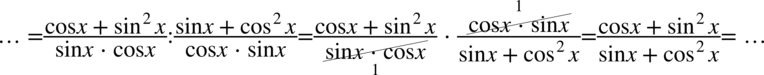
Po prawej stronie, którą usiłujemy otrzymać, w liczniku występują wyłącznie cosinusy, a w mianowniku sinusy. Na szczęście w liczniku i mianowniku występuje sinus oraz cosinus podniesiony do kwadratu, które można zamienić na pożądane elementy korzystając z przekształceń jedynki trygonometrycznej 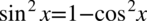 i
i 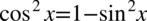 :
: