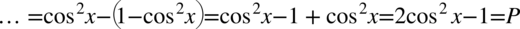Przykład 89
[kliknij aby rozwinąć] 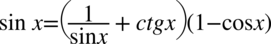
Założenie: 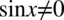 (mianownik nie może być równy
(mianownik nie może być równy  )
)
Będziemy się zajmować prawą stroną, ponieważ jest ona zdecydowanie dłuższa. Na początku pozbędziemy się nawiasów wymnażając kolejno składniki:
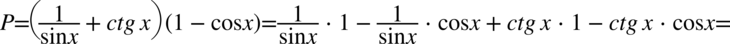

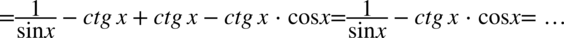
Dla ułatwienia mnożenia zostały użyty zapis 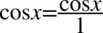 .
.
Po lewej stronie tożsamości nie występuje cotangens, także pozbędziemy się go korzystając ze wzoru 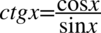 :
:

Dla ułatwienia mnożenia ponownie zostały użyty zapis 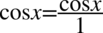 . Powstałe ułamki mają już wspólny mianownik, zatem swobodnie można je zapisać na jednej kresce ułamkowej:
. Powstałe ułamki mają już wspólny mianownik, zatem swobodnie można je zapisać na jednej kresce ułamkowej:
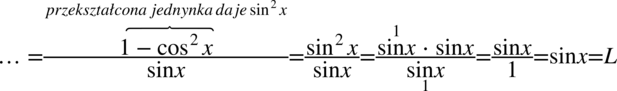

Przykład 90
[kliknij aby rozwinąć] 
Założenie: 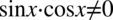 (mianownik nie może być równy
(mianownik nie może być równy  ). Aby iloczyn dwóch składników był różny od zera, każdy składnik z osobna musi być różny od zera, zatem ostatecznie:
). Aby iloczyn dwóch składników był różny od zera, każdy składnik z osobna musi być różny od zera, zatem ostatecznie: 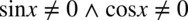
Na wstępie przestrzegam przed skracaniem  . O ile mianownik ułamka jest w idealnej formie pozwalającej na skracanie (znak mnożenia między składnikami), to jednak w liczniku występuje znak odejmowania, który je uniemożliwia. Aby skracanie było prawidłowe minus wraz z otaczającymi go składnikami musi być zamknięty w nawiasie:
. O ile mianownik ułamka jest w idealnej formie pozwalającej na skracanie (znak mnożenia między składnikami), to jednak w liczniku występuje znak odejmowania, który je uniemożliwia. Aby skracanie było prawidłowe minus wraz z otaczającymi go składnikami musi być zamknięty w nawiasie: 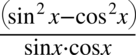 . Po nałożeniu nawiasów nie ma już z czym skrócić cosinusa i sinusa z mianownika (wnętrze nawiasu jest nietykalne, skracać można tylko nawias jako całość).
. Po nałożeniu nawiasów nie ma już z czym skrócić cosinusa i sinusa z mianownika (wnętrze nawiasu jest nietykalne, skracać można tylko nawias jako całość).
Będziemy przekształcać lewą stronę tożsamości, ponieważ występują tu nawiasy oraz tangensy i cotangensy, które łatwo zamienia się na sinusy i cosinusy (występujące po prawej stronie tożsamości) ze wzorów 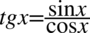 oraz
oraz 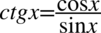 . Można oczywiście zaczynać przekształcanie od prawej strony do lewej, ale tworzenie nawiasów jako ostateczny wynik jest znacznie trudniejsze.
. Można oczywiście zaczynać przekształcanie od prawej strony do lewej, ale tworzenie nawiasów jako ostateczny wynik jest znacznie trudniejsze.
Na początku pozbędziemy się nawiasów kolejno wymnażając składniki:
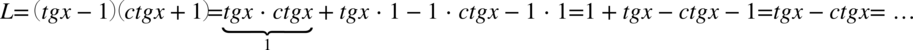
Teraz zamienimy tangens i cotangens na sinusy i cosinusy korzystając ze wzorów 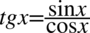 oraz
oraz 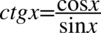 , ponieważ po lewej stronie tożsamości nie występuje żaden tangens ani cotangens:
, ponieważ po lewej stronie tożsamości nie występuje żaden tangens ani cotangens:
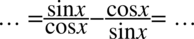
Powstały dwa ułamki, które sprowadzimy do wspólnego mianownika, ponieważ po prawej stronie do której uzyskania dążymy występuje tylko jedna kreska ułamkowa:
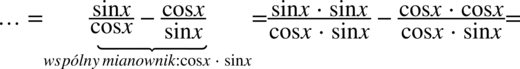
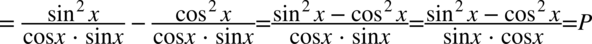

W mianowniku została zmieniona kolejność składników, ponieważ w przypadku mnożenia kolejność składników nie gra roli.
Przykład 91
[kliknij aby rozwinąć] 
Założenie: 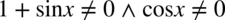 (żaden z mianowników nie może być równy
(żaden z mianowników nie może być równy  ). Po przekształceniu ostatecznie otrzymujemy
). Po przekształceniu ostatecznie otrzymujemy 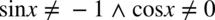 .
.
Lewa strona tożsamości jest dłuższa, zatem to ona będzie przekształcana. Pierwsza czynnością będzie likwidacja tangensa przy użyciu wzoru 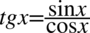 , ponieważ po lewej stronie do której dążymy tangens nie występuje:
, ponieważ po lewej stronie do której dążymy tangens nie występuje:

Powstały dwa ułamki, teraz stworzymy dla nich wspólny mianownik, ponieważ po prawej stronie występuje jeden ułamek:
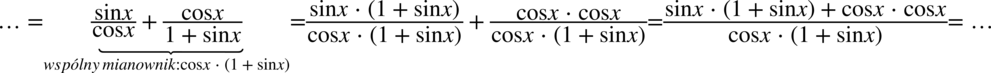
Teraz pozbędziemy się nawiasów w liczniku wymnażając kolejno składniki, natomiast z wymnażaniem mianownika warto się wstrzymać, ponieważ możemy w kolejnych etapach nie zauważyć możliwości skracania, a wymnożyć można zawsze później:
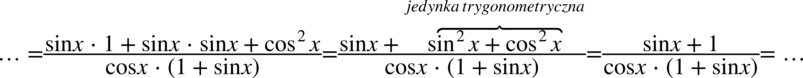
W liczniku powstało identyczne wyrażenie jak nawias w mianowniku, także można spokojnie skrócić obydwa wyrażenia:
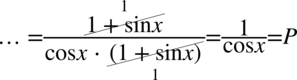

Przykład 92
[kliknij aby rozwinąć] 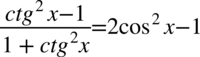
Założenie: 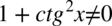 (mianownik nie może być równy
(mianownik nie może być równy  ). Po przekształceniu założenia otrzymujemy
). Po przekształceniu założenia otrzymujemy 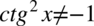 - co jest zawsze prawdą, ponieważ dowolna liczba lub wyrażenie podniesiona do kwadratu nigdy nie będzie liczbą ujemną. Ostatecznie w związku z tym można zapisać
- co jest zawsze prawdą, ponieważ dowolna liczba lub wyrażenie podniesiona do kwadratu nigdy nie będzie liczbą ujemną. Ostatecznie w związku z tym można zapisać 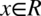 , bo niezależnie od wartości kąta cotangens podniesiony do kwadratu nie będzie ujemny.
, bo niezależnie od wartości kąta cotangens podniesiony do kwadratu nie będzie ujemny.
Znów uprzedzam przed „radosnym” skracaniem w stylu: 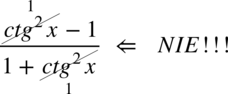 . Aby skracanie było możliwe znak dodawania lub odejmowania musi być zamknięty wraz z okalającymi go elementami w nawiasie:
. Aby skracanie było możliwe znak dodawania lub odejmowania musi być zamknięty wraz z okalającymi go elementami w nawiasie: 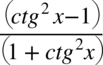 . Po zamknięciu w nawiasie nie ma już elementów do skracania. Oczywiście pamiętamy, że pojedynczych elementów z wnętrza nawiasów nie wolno skracać. Skróceniu ulega wyłącznie cała zawartość nawiasów o ile jest identyczna.
. Po zamknięciu w nawiasie nie ma już elementów do skracania. Oczywiście pamiętamy, że pojedynczych elementów z wnętrza nawiasów nie wolno skracać. Skróceniu ulega wyłącznie cała zawartość nawiasów o ile jest identyczna.
Lewa strona tożsamości jest dłuższa, poza tym występują tu cotangensy, które łatwo przekształcić na sinusy i cosinusy, także to lewa strona będzie podlegać przekształceniom. Na początku pozbędziemy się cotangensów korzystając ze wzoru 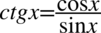 , ponieważ po lewej stronie do której uzyskania dążymy cotangensy nie występują:
, ponieważ po lewej stronie do której uzyskania dążymy cotangensy nie występują:
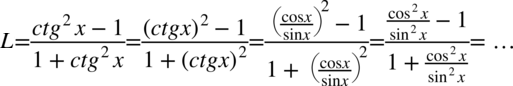
Teraz do powstałych ułamków „wrzucimy” jedynki sprowadzając je do wspólnego mianownika, dla ułatwienia działań użyjemy zapisu  (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie):
nie ulega zmianie):
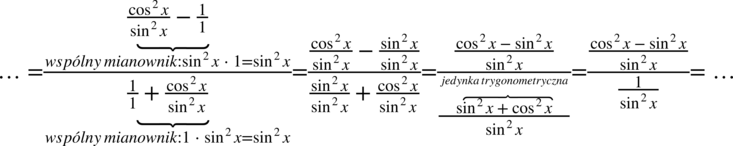
Kolejnym krokiem będzie zlikwidowanie piętrowego ułamka poprzez zamianę kreski ułamkowej na znak dzielenia, a następnie zamiana dzielenia na mnożenie przez odwrotność dzielnika:
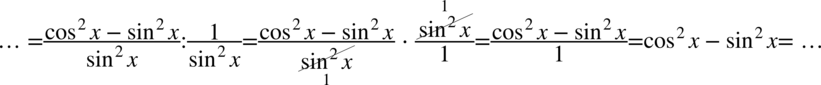
Po prawej stronie do której dążymy występuje wyłącznie cosinus, także pozbędziemy się sinusa korzystając ze wzoru na przekształconą jedynkę trygonometryczną 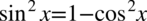 , pamiętajmy o zastosowaniu nawiasów, aby nie zgubić znaków:
, pamiętajmy o zastosowaniu nawiasów, aby nie zgubić znaków: