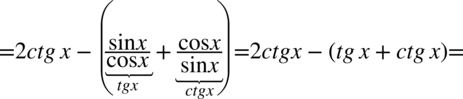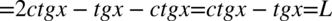Przykład 85
[kliknij aby rozwinąć] 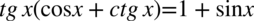
Lewa strona jest dłuższa, zatem to ona będzie przekształcana. Na początku pozbędziemy się nawiasu wymnażając kolejno składniki:
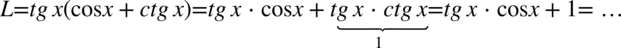
Teraz pozbędziemy się tangensa korzystając ze wzoru 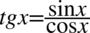 , ponieważ po prawej stronie tożsamości nie ma tangensów:
, ponieważ po prawej stronie tożsamości nie ma tangensów:
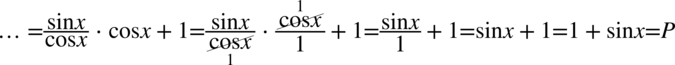

Przy skracaniu został użyty zapis 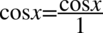 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez  nie ulega zmianie, a zapis ten rozwiewa wiele wątpliwości dotyczących działań na ułamkach.
nie ulega zmianie, a zapis ten rozwiewa wiele wątpliwości dotyczących działań na ułamkach.
Przykład 86
[kliknij aby rozwinąć] 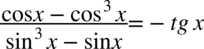
Założenie: 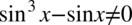 (mianownik nie może być równy
(mianownik nie może być równy  ). Przekształcając założenie możemy wyciągnąć
). Przekształcając założenie możemy wyciągnąć 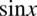 przed nawias co daje
przed nawias co daje 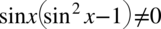 . Warto też rozpisać powstały nawias ze wzoru skróconego mnożenia
. Warto też rozpisać powstały nawias ze wzoru skróconego mnożenia 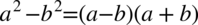 :
:
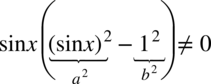
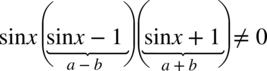
Otrzymujemy: 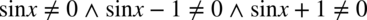 (każdy z czynników musi być różny od zera, ponieważ iloczyn trzech składników będzie równy od zera tylko wtedy, gdy każdy z nich będzie różny od zera – każda liczba wymnożona przez
(każdy z czynników musi być różny od zera, ponieważ iloczyn trzech składników będzie równy od zera tylko wtedy, gdy każdy z nich będzie różny od zera – każda liczba wymnożona przez  daje
daje  )
)
Wykonujemy ostatnie przekształcenia i otrzymujemy: 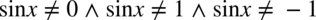 .
.
Lewa strona równości jest dłuższa, zatem to ona będzie przekształcana. Przyglądając się licznikowi i mianownikowi ułamka nie zauważamy nic nadzwyczajnego (żadnych znanych wzorów), ale można w liczniku wyciągnąć przed nawias  , a w mianowniku
, a w mianowniku 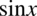 :
:
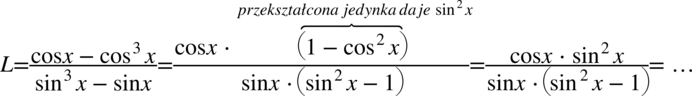
Zawartość nawiasu w mianowniku przypomina wzór 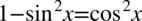 , ale różni od niego znakami występującymi przed kolejnymi składnikami. Jeżeli mamy taką sytuację, to trzeba wyciągnąć minus przed nawias. Na początku zmienię kolejność składników w nawiasie, a następnie wyciągnę minus przed nawias co zmieni znaki w nawiasie na przeciwne:
, ale różni od niego znakami występującymi przed kolejnymi składnikami. Jeżeli mamy taką sytuację, to trzeba wyciągnąć minus przed nawias. Na początku zmienię kolejność składników w nawiasie, a następnie wyciągnę minus przed nawias co zmieni znaki w nawiasie na przeciwne:
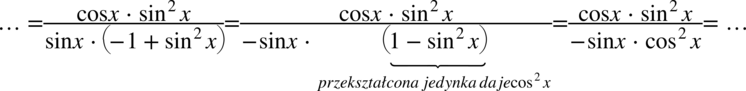
Teraz rozpiszemy kwadraty sinusów i cosinusów i skrócimy odpowiednie składniki, w tym przypadku mamy komfortową sytuację do skracania, ponieważ w liczniku i mianowniku występuje wyłącznie mnożenie:
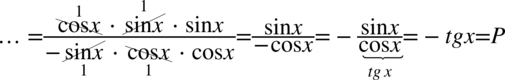

Zapisy  są równoznaczne. Jeżeli w ułamku występuje jeden minus, to można go swobodnie umieścić albo w liczniku albo w mianowniku, albo przed ułamkiem. Jeżeli minus stoi przed ułamkiem wędruje albo do licznika albo do mianownika – nigdy do obu naraz!
są równoznaczne. Jeżeli w ułamku występuje jeden minus, to można go swobodnie umieścić albo w liczniku albo w mianowniku, albo przed ułamkiem. Jeżeli minus stoi przed ułamkiem wędruje albo do licznika albo do mianownika – nigdy do obu naraz!
Przykład 87
[kliknij aby rozwinąć] 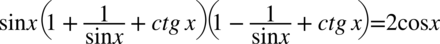
Założenie: 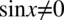 (mianownik nie może być równy
(mianownik nie może być równy  )
)
Zdecydowanie lewa strona tożsamości jest dłuższa, zatem to ona będzie przekształcana. Na początku pozbędziemy się nawiasów kolejno wymnażając składniki. Mamy tu trzy elementy do wymnożenia: 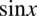 oraz zawartość dwóch nawiasów. W mnożeniu mamy dowolność co do kolejności mnożenia: albo pierwszy element z drugim, albo pierwszy z trzecim, albo drugi z trzecim, nie ma to większego znaczenia. Natomiast bardzo ważną kwestią jest zapisanie wyniku pierwszego mnożenia w nawiasie, ponieważ do wymnożenia zostanie jeszcze jeden element, który trzeba wymnożyć przez całość wyniku uzyskanego z pierwszego mnożenia. Wymnożę na początku
oraz zawartość dwóch nawiasów. W mnożeniu mamy dowolność co do kolejności mnożenia: albo pierwszy element z drugim, albo pierwszy z trzecim, albo drugi z trzecim, nie ma to większego znaczenia. Natomiast bardzo ważną kwestią jest zapisanie wyniku pierwszego mnożenia w nawiasie, ponieważ do wymnożenia zostanie jeszcze jeden element, który trzeba wymnożyć przez całość wyniku uzyskanego z pierwszego mnożenia. Wymnożę na początku 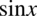 przez zawartość pierwszego nawiasu, a później uzyskany wynik przez trzeci nawias:
przez zawartość pierwszego nawiasu, a później uzyskany wynik przez trzeci nawias:
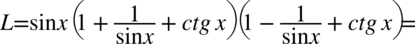
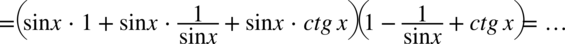
Dla ułatwienia skracania zostanie zastosowany zapis 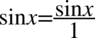 ( każda liczba podzielona przez
( każda liczba podzielona przez  nie ulega zmianie):
nie ulega zmianie):
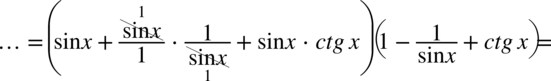
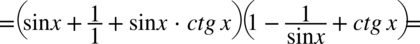
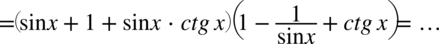
Teraz wymnożymy zawartość dwóch powstałych nawiasów:
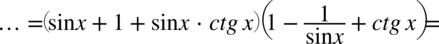
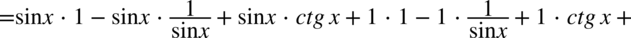
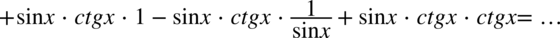
Dla ułatwienia skracania znowu zostanie zastosowany zapis 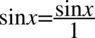 :
:
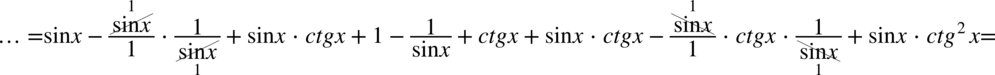
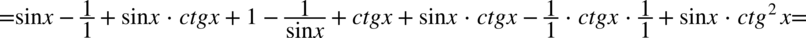
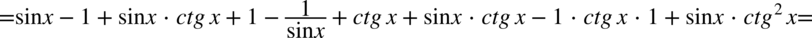
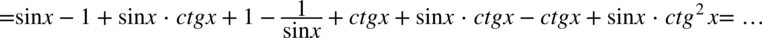
Dokonamy redukcji wyrazów podobnych:
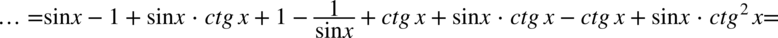

Teraz pozbędziemy się cotangensa korzystając ze wzoru 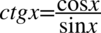 , ponieważ po prawej stronie do której uzyskania dążymy nie ma cotangensa:
, ponieważ po prawej stronie do której uzyskania dążymy nie ma cotangensa:


I znowu skorzystamy z zapisu 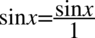 :
:
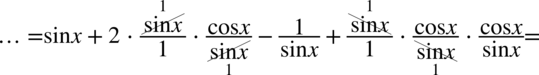
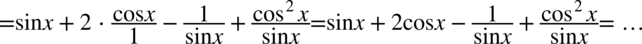
Teraz zapiszemy na jednej kresce ułamkowej dwa ułamki z końcówki przykładu, dla ułatwienia minus występujący przed przedostatnim ułamkiem „wrzucimy” do licznika:
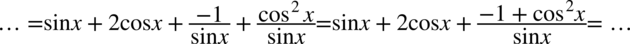
To co otrzymaliśmy w liczniku bardzo przypomina wzór na przekształconą jedynkę trygonometryczną  , ale nie zgadzają się znaki. Aby uzyskać ten wzór wystarczy wyciągnąć minus przed nawias co zmieni znaki na pożądane:
, ale nie zgadzają się znaki. Aby uzyskać ten wzór wystarczy wyciągnąć minus przed nawias co zmieni znaki na pożądane:
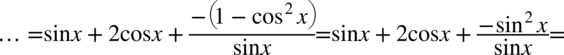
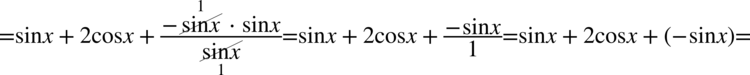


Przykład 88
[kliknij aby rozwinąć] 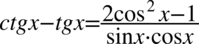
Założenie: 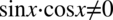 (mianownik nie może być równy
(mianownik nie może być równy  ). Aby iloczyn dwóch składników był różny od zera, każdy składnik z osobna musi być różny od zera, zatem ostatecznie:
). Aby iloczyn dwóch składników był różny od zera, każdy składnik z osobna musi być różny od zera, zatem ostatecznie: 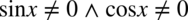 .
.
Na wstępie przestrzegam przed skracaniem 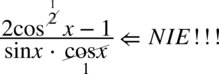 . O ile mianownik ułamka jest w idealnej formie pozwalającej na skracanie (znak mnożenia między składnikami), to jednak w liczniku występuje znak odejmowania, który je uniemożliwia. Aby skracanie było prawidłowe minus wraz z otaczającymi go składnikami musi być zamknięty w nawiasie:
. O ile mianownik ułamka jest w idealnej formie pozwalającej na skracanie (znak mnożenia między składnikami), to jednak w liczniku występuje znak odejmowania, który je uniemożliwia. Aby skracanie było prawidłowe minus wraz z otaczającymi go składnikami musi być zamknięty w nawiasie: 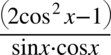 . Po nałożeniu nawiasów nie ma już z czym skrócić cosinusa z mianownika (wnętrze nawiasu jest nietykalne).
. Po nałożeniu nawiasów nie ma już z czym skrócić cosinusa z mianownika (wnętrze nawiasu jest nietykalne).
Podaną tożsamość można udowodnić na dwa sposoby:
I sposób
Zajmiemy się lewą stroną, gdzie zamienimy tangens i cotangens na sinusy i cosinusy korzystając ze wzorów 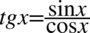 oraz
oraz 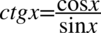 , ponieważ po lewej stronie tożsamości nie występuje żaden tangens ani cotangens:
, ponieważ po lewej stronie tożsamości nie występuje żaden tangens ani cotangens:

Powstały dwa ułamki, które sprowadzimy do wspólnego mianownika, ponieważ po prawej stronie do której uzyskania dążymy występuje tylko jedna kreska ułamkowa:
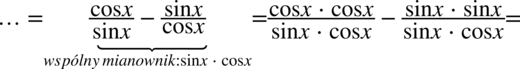
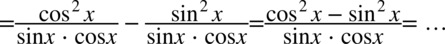
Powstały mianownik odpowiada prawej stronie tożsamości, natomiast w liczniku musimy pozbyć się sinusa, bo po prawej stronie tożsamości nie występuje, ale mając sinus podniesiony do kwadratu bez problemu można zamienić go na cosinus korzystając ze wzoru na przekształconą jedynkę trygonometryczną 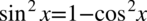 . Przy zamianie pamiętajmy o nawiasie, aby nie pogubić znaków:
. Przy zamianie pamiętajmy o nawiasie, aby nie pogubić znaków:


II sposób
Tym razem zajmiemy się prawą stroną, ten sposób jest trudniejszy i wymaga większej ilości przekształceń. Na początku rozdzielmy ułamek na dwa, analogicznie jak wykonuje się to na ułamkach zwykłych np. 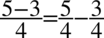 . Czynność ta pozwoli nam na uzyskanie dwóch oddzielnych składników, które mamy po lewej stronie tożsamości:
. Czynność ta pozwoli nam na uzyskanie dwóch oddzielnych składników, które mamy po lewej stronie tożsamości:
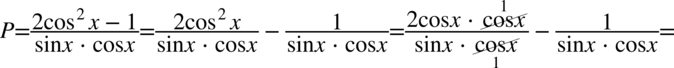
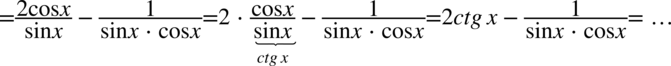
Skracanie było możliwe, ponieważ po rozdzieleniu na dwa ułamki w każdym z nich występowało wyłącznie mnożenie pomiędzy składnikami.
Jedynym sposobem zlikwidowania ułamka, który pozostał na tym etapie jest rozpisanie jedynki ze wzoru 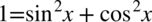 :
:

Teraz znowu rozdzielimy powstały ułamek na dwa analogicznie jak wykonuje się to na ułamkach zwykłych np. 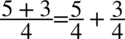 . Tutaj zapiszemy ułamki po rozdzieleniu w nawiasie, ponieważ przed nierozdzielonym ułamkiem stoi minus, który zmieni znaki. Jeśli nie użyjemy nawiasu, prawdopodobnie zapomnimy o tej zmianie i wynik będzie nieprawidłowy.
. Tutaj zapiszemy ułamki po rozdzieleniu w nawiasie, ponieważ przed nierozdzielonym ułamkiem stoi minus, który zmieni znaki. Jeśli nie użyjemy nawiasu, prawdopodobnie zapomnimy o tej zmianie i wynik będzie nieprawidłowy.