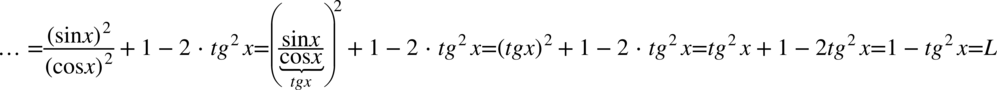Przykład 81
[kliknij aby rozwinąć] 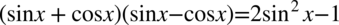
Po lewej stronie tożsamości występują nawiasy, więc pierwszą wykonaną czynnością będzie ich likwidacja. Można to wykonać poprzez wymnożenie kolejnych składników, ale warto przyjrzeć się zawartości nawiasów – są identyczne poza znakiem występującym pośrodku, także można użyć tu wzoru skróconego postaci 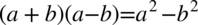 :
:

Po prawej stronie tożsamości, do której uzyskania dążymy nie ma cosinusa, ale mając cosinus podniesiony do kwadratu bez problemu można zamienić go na sinus korzystając ze wzoru na przekształconą jedynkę trygonometryczną 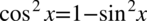 . Przy zamianie pamiętajmy o nawiasie, aby nie pogubić znaków:
. Przy zamianie pamiętajmy o nawiasie, aby nie pogubić znaków:
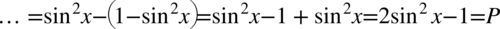

Przykład 82
[kliknij aby rozwinąć] 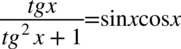
Założenie: 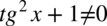 (mianownik nie może być równy
(mianownik nie może być równy  ). Po przekształceniu założenia otrzymujemy
). Po przekształceniu założenia otrzymujemy 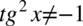 - co jest zawsze prawdą, ponieważ dowolna liczba lub wyrażenie podniesiona do kwadratu nigdy nie będzie liczbą ujemną. Ostatecznie w związku z tym można zapisać
- co jest zawsze prawdą, ponieważ dowolna liczba lub wyrażenie podniesiona do kwadratu nigdy nie będzie liczbą ujemną. Ostatecznie w związku z tym można zapisać 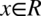 , bo niezależnie od wartości kąta tangens podniesiony do kwadratu nie będzie ujemny.
, bo niezależnie od wartości kąta tangens podniesiony do kwadratu nie będzie ujemny.
Znów uprzedzam przed „radosnym” skracaniem w stylu: 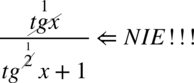 . Aby skracanie było możliwe znak dodawania lub odejmowania musi być zamknięty wraz z okalającymi go elementami w nawiasie:
. Aby skracanie było możliwe znak dodawania lub odejmowania musi być zamknięty wraz z okalającymi go elementami w nawiasie: 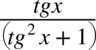 . Po zamknięciu w nawiasie nie ma już elementów do skracania. Oczywiście pamiętamy, że pojedynczych elementów z wnętrza nawiasów nie wolno skracać. Skróceniu ulega wyłącznie cała zawartość nawiasów o ile jest identyczna.
. Po zamknięciu w nawiasie nie ma już elementów do skracania. Oczywiście pamiętamy, że pojedynczych elementów z wnętrza nawiasów nie wolno skracać. Skróceniu ulega wyłącznie cała zawartość nawiasów o ile jest identyczna.
Lewa strona tożsamości jest dłuższa i to ona będzie przekształcana. Poza tym występuje tu tangens, który można spokojnie rozpisać na sinus i cosinus ze wzoru 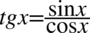 , które mamy po prawej stronie tożsamości:
, które mamy po prawej stronie tożsamości:
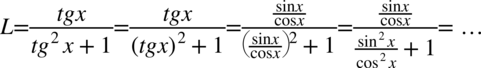
Teraz wciągniemy jedynkę z dołu na kreskę ułamkową poprzez sprowadzenie do wspólnego mianownika, dla ułatwienia zostanie użyty zapis 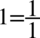 , bo każda liczba podzielona przez jeden nie ulega zmianie:
, bo każda liczba podzielona przez jeden nie ulega zmianie:

Teraz pozbędziemy się piętrowego ułamka zamieniając główną kreskę ułamkową na znak dzielenia, a później analogicznie jak na ułamkach zwykłych zastępując dzielenie mnożeniem przez odwrotność drugiego składnika (tzw. dzielnika):
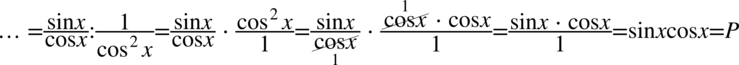

Skracanie było możliwe, ponieważ w liczniku i mianowniku było wyłącznie mnożenie.
Przykład 83
[kliknij aby rozwinąć] 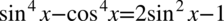
W tym przykładzie obie strony mają podobną długość, jednak po lewej stronie występują wyższe wartości potęg i to właśnie lewa strona będzie przekształcana. Trzeba się tu wykazać znajomością wzorów skróconego mnożenia. Na początku zapiszemy czwórki z wykładników potęg za pomocą dwójek, ponieważ po prawej stronie znajdują się właśnie dwójki:
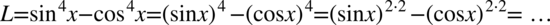
Następnie skorzystamy z własności potęg, gdzie  :
:
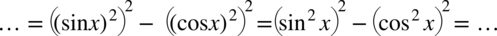
Teraz przyjrzyjmy się powstałemu wynikowi - mamy dwa elementy poniesione do kwadratu, które są oddzielone znakiem minus. I w tym momencie trzeba użyć wzoru skróconego mnożenia 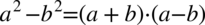 do rozłożenia powstałego wyrażenia na czynniki (czyli iloczyn nawiasów):
do rozłożenia powstałego wyrażenia na czynniki (czyli iloczyn nawiasów):
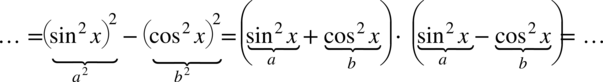
Teraz przyjrzyjmy się zawartości nawiasów, w pierwszym z nich otrzymaliśmy jedynkę trygonometryczną:
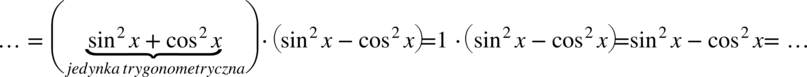
Po prawej stronie tożsamości, do której uzyskania dążymy nie ma cosinusa, ale mając cosinus podniesiony do kwadratu bez problemu można zamienić go na sinus korzystając ze wzoru na przekształconą jedynkę trygonometryczną 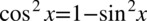 . Przy zamianie pamiętajmy o nawiasie, aby nie pogubić znaków:
. Przy zamianie pamiętajmy o nawiasie, aby nie pogubić znaków:
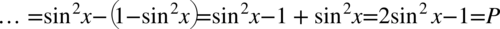

Przykład 84
[kliknij aby rozwinąć] 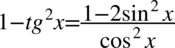
Założenie: 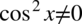 (mianownik nie może być równy
(mianownik nie może być równy  ). Ostatecznie otrzymujemy
). Ostatecznie otrzymujemy 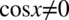 , ponieważ jeżeli cosinus jest różny od zera, to tym bardziej cosinus podniesiony do kwadratu będzie różny od zera.
, ponieważ jeżeli cosinus jest różny od zera, to tym bardziej cosinus podniesiony do kwadratu będzie różny od zera.
Podaną równość można udowodnić na dwa sposoby:
I sposób
Zajmiemy się lewą stroną, mimo że wydaje się krótsza, ale występuje tu tangens, który można zlikwidować korzystając ze wzoru 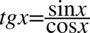 . Poza tym po prawej stronie, do której uzyskania dążymy nie ma żadnego tangensa:
. Poza tym po prawej stronie, do której uzyskania dążymy nie ma żadnego tangensa:
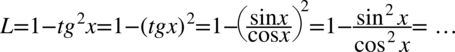
Znów przyjrzyjmy się prawej stronie, która w całości jest ułamkiem, tak więc  musimy wrzucić na kreskę ułamkową poprzez sprowadzenie do wspólnego mianownika. Dla ułatwienia działań zostanie użyty zapis
musimy wrzucić na kreskę ułamkową poprzez sprowadzenie do wspólnego mianownika. Dla ułatwienia działań zostanie użyty zapis 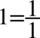 (każda liczna podzielona przez
(każda liczna podzielona przez  nie ulega zmianie):
nie ulega zmianie):
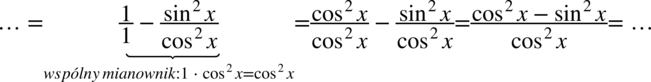
Po prawej stronie tożsamości nie ma cosinusa w liczniku, ale mając cosinus podniesiony do kwadratu bez problemu można zamienić go na sinus korzystając ze wzoru na przekształconą jedynkę trygonometryczną 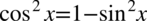 . Przy zamianie pamiętajmy o nawiasie, aby nie pogubić znaków, w tym przypadku nie są one niezbędne, ale przezorny zawsze ubezpieczony:
. Przy zamianie pamiętajmy o nawiasie, aby nie pogubić znaków, w tym przypadku nie są one niezbędne, ale przezorny zawsze ubezpieczony:
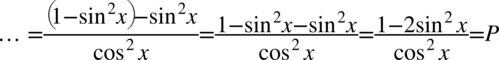

II sposób
Tym razem zaczniemy od prawej strony. Sposób ten może wydać się nieco karkołomny. Na początku rozdzielmy ułamek na dwa, analogicznie jak wykonuje się to na ułamkach zwykłych np. 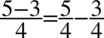 . Czynność ta pozwoli nam na uzyskanie dwóch oddzielnych składników, które mamy po lewej stronie tożsamości:
. Czynność ta pozwoli nam na uzyskanie dwóch oddzielnych składników, które mamy po lewej stronie tożsamości:
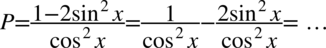
Na razie zajmiemy się drugim nowo powstałym ułamkiem i korzystając z własności potęg 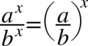 oraz wzoru
oraz wzoru 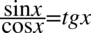 stworzymy tangens do kwadratu:
stworzymy tangens do kwadratu:
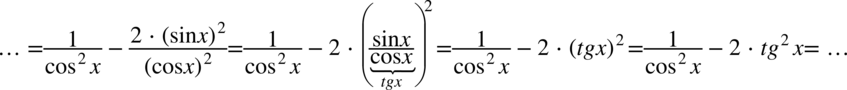
Uzyskaliśmy tangens podniesiony do kwadratu, ale przeszkadza nam jeszcze dwójka i 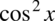 w mianowniku pierwszego ułamka. Teraz rozbijemy jedynkę z pierwszego ułamka korzystając ze wzoru na jedynkę trygonometryczną, bo nie ma tu innego wyjścia pozwalającego na zlikwidowanie tego ułamka:
w mianowniku pierwszego ułamka. Teraz rozbijemy jedynkę z pierwszego ułamka korzystając ze wzoru na jedynkę trygonometryczną, bo nie ma tu innego wyjścia pozwalającego na zlikwidowanie tego ułamka:
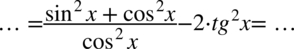
Na tym etapie nie wolno skracać cosinusów z licznika i mianownika, ponieważ w liczniku występuje dodawanie pomiędzy składnikami!
Teraz znowu rozdzielimy powstały ułamek na dwa analogicznie jak wykonuje się to na ułamkach zwykłych np.  :
:
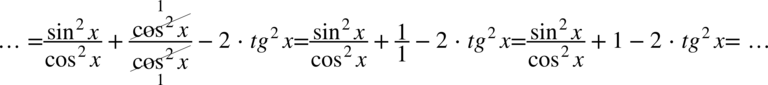
Po rozdzieleniu ułamka skracanie było możliwe, ponieważ ani w liczniku ani w mianowniku nie było już dodawania.
Na końcu znów skorzystamy z własności potęg 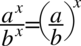 oraz wzoru
oraz wzoru 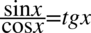 i stworzymy tangens do kwadratu:
i stworzymy tangens do kwadratu: