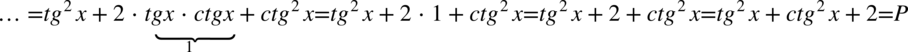Przykład 77
[kliknij aby rozwinąć] 
Założenie: 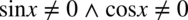 (żaden mianownik nie może być równy
(żaden mianownik nie może być równy  ).
).
Lewa strona tożsamości jest zdecydowanie dłuższa, zatem to ona będzie przekształcana. Na początku pozbędziemy się nawiasów wymnażając kolejno składniki:
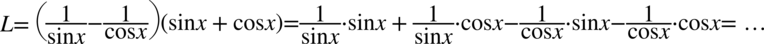
Aby rozwiać wątpliwości odnośnie mnożenia przez górę czy dół ułamka lub skracania zostanie zastosowany zapis 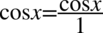 oraz
oraz 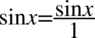 , ponieważ jakakolwiek liczba czy znak podzielony przez
, ponieważ jakakolwiek liczba czy znak podzielony przez  nie ulega zmianie:
nie ulega zmianie:
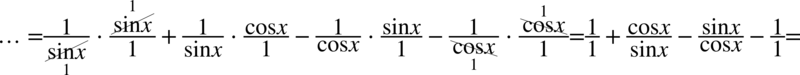


Przykład 78
[kliknij aby rozwinąć] 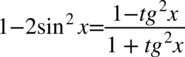
Założenie: 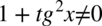 (mianownik nie może być równy
(mianownik nie może być równy  ). Po przekształceniu założenia otrzymujemy
). Po przekształceniu założenia otrzymujemy 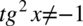 - co jest zawsze prawdą, ponieważ dowolna liczba lub wyrażenie podniesiona do kwadratu nigdy nie będzie liczbą ujemną. Ostatecznie w związku z tym można zapisać
- co jest zawsze prawdą, ponieważ dowolna liczba lub wyrażenie podniesiona do kwadratu nigdy nie będzie liczbą ujemną. Ostatecznie w związku z tym można zapisać 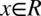 , bo niezależnie od wartości kąta tangens podniesiony do kwadratu nie będzie ujemny.
, bo niezależnie od wartości kąta tangens podniesiony do kwadratu nie będzie ujemny.
Znów uprzedzam przed „radosnym” skracaniem w stylu: 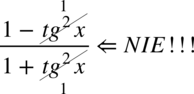 . Aby skracanie było możliwe znak dodawania lub odejmowania musi być zamknięty wraz z okalającymi go elementami w nawiasie:
. Aby skracanie było możliwe znak dodawania lub odejmowania musi być zamknięty wraz z okalającymi go elementami w nawiasie: 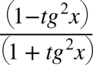 . Po zamknięciu w nawiasie nie ma już elementów do skracania. Oczywiście pamiętamy, że pojedynczych elementów z wnętrza nawiasów nie wolno skracać. Skróceniu ulega wyłącznie cała zawartość nawiasów o ile jest identyczna.
. Po zamknięciu w nawiasie nie ma już elementów do skracania. Oczywiście pamiętamy, że pojedynczych elementów z wnętrza nawiasów nie wolno skracać. Skróceniu ulega wyłącznie cała zawartość nawiasów o ile jest identyczna.
Prawa strona tożsamości jest dłuższa, poza tym występują tu tangensy, które łatwo przekształcić w sinusy i cosinusy, także to prawa strona będzie podlegać przekształceniom. Na początku pozbędziemy się tangensów korzystając ze wzoru 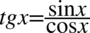 , ponieważ po lewej stronie do której uzyskania dążymy tangensy nie występują:
, ponieważ po lewej stronie do której uzyskania dążymy tangensy nie występują:
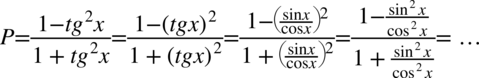
Teraz do powstałych ułamków „wrzucimy” jedynki sprowadzając je do wspólnego mianownika, dla ułatwienia działań użyjemy zapisu 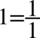 (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie):
nie ulega zmianie):

Kolejnym krokiem będzie zlikwidowanie piętrowego ułamka poprzez zamianę kreski ułamkowej na znak dzielenia, a następnie zamiana dzielenia na mnożenie przez odwrotność dzielnika:
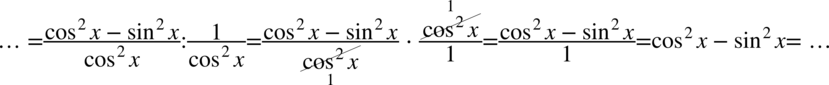
Po lewej stronie do której dążymy występuje wyłącznie sinus, także pozbędziemy się cosinusa korzystając ze wzoru na przekształconą jedynkę trygonometryczną 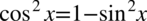 :
:


Przykład 79
[kliknij aby rozwinąć] 
Po lewej stronie równości występuje nawias, także mamy tu większe możliwości manewru. Pozbędziemy się nawiasu korzystając ze wzoru skróconego mnożenia 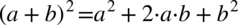 :
:
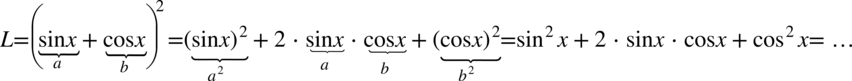
Po prawej stronie, do której uzyskania dążymy występuje jedynka, a w przykładzie uzyskaliśmy sinus i cosinus podniesiony do kwadratu, warto te dwa elementy do siebie „przytulać”, ponieważ tworzą jedynkę trygonometryczną. Tak więc zmienimy kolejność składników:
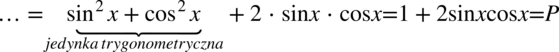

Przykład 80
[kliknij aby rozwinąć] 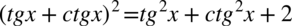
Po lewej stronie równości występuje nawias, także mamy tu większe możliwości manewru. Na początku pozbędziemy się nawiasu korzystając ze wzoru skróconego mnożenia 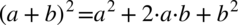 :
:
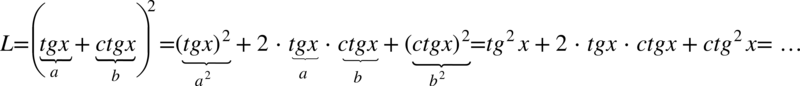
Na koniec skorzystamy ze wzoru 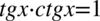 i zmienimy kolejność składników tak aby otrzymać prawą stronę tożsamości:
i zmienimy kolejność składników tak aby otrzymać prawą stronę tożsamości: