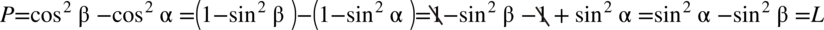Przykład 5
[kliknij aby rozwinąć] 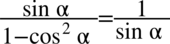
Założenie: 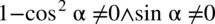 (żaden mianownik nie może być równy
(żaden mianownik nie może być równy  )
)
Po przekształceniu założenia 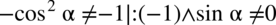
otrzymujemy 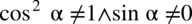 . Jaką wartość musi mieć cosinus, aby podniesiony do kwadratu dał
. Jaką wartość musi mieć cosinus, aby podniesiony do kwadratu dał  ? Oczywiście
? Oczywiście  , ale nie można zapomnieć o
, ale nie można zapomnieć o  , bo
, bo 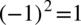 .
.
Ostatecznie założenie wygląda następująco:
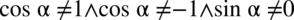
Lewa strona równości jest nieco dłuższa od prawej, zatem to nią będziemy się zajmować. W mianowniku znajduje się przekształcona „jedynka trygonometryczna”, czyli 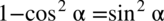 :
:
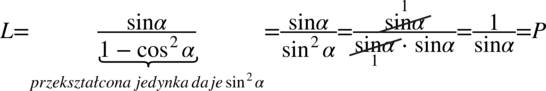

Tu można było skracać bez obaw, ponieważ w ułamku między składnikami występuje znak mnożenia.
Przykład 6
[kliknij aby rozwinąć] 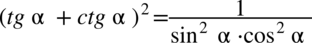
Założenie: 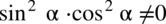 (mianownik nie może być równy
(mianownik nie może być równy  )
)
Jeżeli mamy wymnożone przez siebie dwa wyrażenia (u nas to
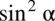 oraz
oraz
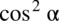 )
, a ich iloczyn ma być różny od zera, to żadne z nich nie może być równe
)
, a ich iloczyn ma być różny od zera, to żadne z nich nie może być równe
 , ponieważ
, ponieważ
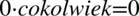 , zatem otrzymujemy:
, zatem otrzymujemy:
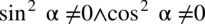
Po przekształceniu założenia otrzymujemy ostatecznie 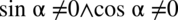 , bo jeżeli cosinus (sinus) będzie wynosił
, bo jeżeli cosinus (sinus) będzie wynosił  , to także cosinus (sinus) podniesiony do kwadratu będzie równy
, to także cosinus (sinus) podniesiony do kwadratu będzie równy  ) .
) .
Zajmiemy się lewą stroną. Występuje tu nawias podniesiony do kwadratu, zatem pierwszy krok to skorzystanie ze wzoru skróconego mnożenia 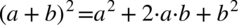 .
.
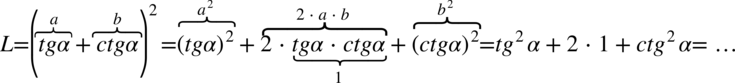
Po prawej stronie równości występuje sinus i cosinus, zatem kolejny krok to skorzystanie ze wzorów 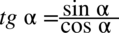 oraz
oraz 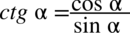 :
:
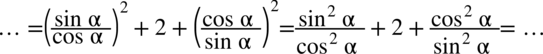
Jednoczenie poprzez zastosowanie tych dwóch wzorów powstają kreski ułamkowe, które trzeba będzie przekształcić w jedną (występuje po prawej stronie) stosując wspólny mianownik. Dla ułatwienia rachunków zastosowano zapis 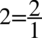 , bo każda liczba podzielona przez
, bo każda liczba podzielona przez  nie ulega zmianie.
nie ulega zmianie.
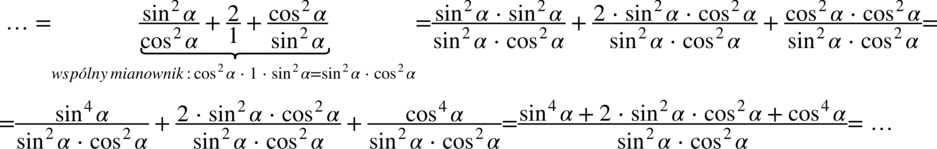
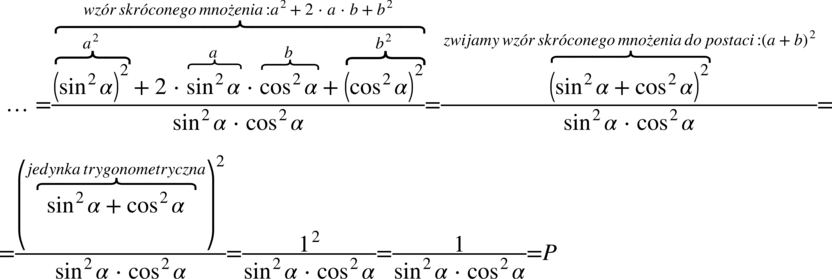
Teraz najtrudniejsza część. Przyjrzyjmy się dokładniej licznikowi naszego ułamka. Występuje tu wzór skróconego mnożenia postaci 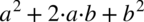 , który należy zwinąć do postaci
, który należy zwinąć do postaci 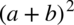 . Aby lepiej zobaczyć dany wzór skorzystamy z własności potęg:
. Aby lepiej zobaczyć dany wzór skorzystamy z własności potęg:
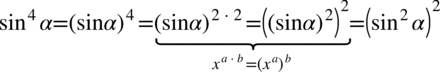
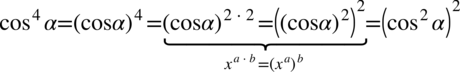

Przykład 7
[kliknij aby rozwinąć] 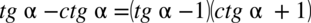
Po prawej stronie równości występują nawiasy, zatem mamy tu większe możliwości do wykonania jakichkolwiek przekształceń. Na początku pozbędziemy się nawiasów wymnażając ze sobą kolejne elementy. Nie ma tu potrzeby zamiany tangensa i cotangensa na sinus i cosinus, ponieważ po lewej stronie nie występują.
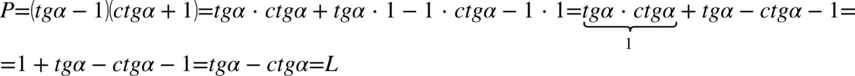

Przykład 8
[kliknij aby rozwinąć] 
Obie strony równości są identycznej długości. Można je sprawdzić na dwojako:
I sposób
Zaczniemy przekształcenia od lewej strony, występują tu sinusy podniesione do kwadratu dwóch kątów 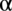 oraz
oraz  , po drugiej stronie występują cosinusy również podniesione do kwadratu, zatem można je przekształcić ze wzorów
, po drugiej stronie występują cosinusy również podniesione do kwadratu, zatem można je przekształcić ze wzorów 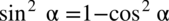 oraz
oraz 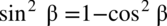 . Pamiętajmy o nawiasach aby nie zgubić znaków przy późniejszych obliczeniach:
. Pamiętajmy o nawiasach aby nie zgubić znaków przy późniejszych obliczeniach:
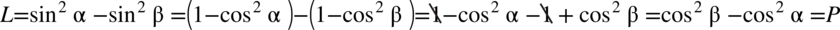

II sposób
Zaczniemy przekształcenia od prawej strony, występują tu cosinusy podniesione do kwadratu dwóch kątów 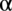 oraz
oraz  , po drugiej stronie występują sinusy również podniesione do kwadratu, zatem można je przekształcić ze wzorów
, po drugiej stronie występują sinusy również podniesione do kwadratu, zatem można je przekształcić ze wzorów 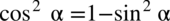 oraz
oraz 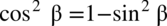 . Pamiętajmy o nawiasach aby nie zgubić znaków przy późniejszych obliczeniach:
. Pamiętajmy o nawiasach aby nie zgubić znaków przy późniejszych obliczeniach: