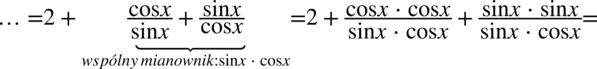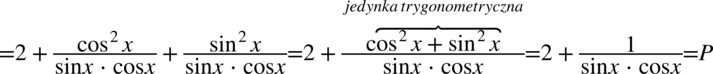Przykład 73
[kliknij aby rozwinąć] 
W tym przykładzie obie strony mają podobną długość, jednak po lewej stronie występują wyższe wartości potęg i to właśnie lewa strona będzie przekształcana. Trzeba się tu wykazać znajomością wzorów skróconego mnożenia. Na początku zapiszemy czwórki z wykładników potęg za pomocą dwójek, ponieważ po prawej stronie znajdują się właśnie dwójki:

Teraz skorzystamy z własności potęg, gdzie  :
:
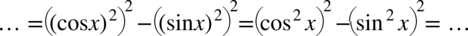
Teraz przyjrzyjmy się powstałemu wynikowi - mamy dwa elementy poniesione do kwadratu, które są oddzielone znakiem minus. I w tym momencie trzeba użyć wzoru skróconego mnożenia 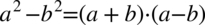 do rozłożenia powstałego wyrażenia na czynniki (czyli iloczyn nawiasów):
do rozłożenia powstałego wyrażenia na czynniki (czyli iloczyn nawiasów):
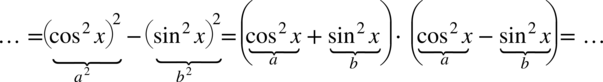
Teraz przyjrzyjmy się zawartości nawiasów, w pierwszym z nich otrzymaliśmy jedynkę trygonometryczną:
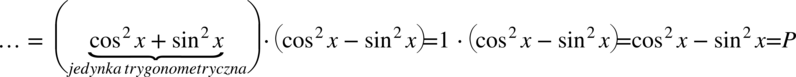

Przykład 74
[kliknij aby rozwinąć] 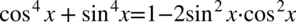
Przykład dość specyficzny w dowodzeniu, ponieważ trzeba tu wykonać trik polegający na dopisaniu pewnego wyrażenia aby otrzymać wzór skróconego mnożenia. Oczywiście dopisane wyrażenie należy odjąć, ponieważ wartość strony tożsamości nie może ulec zmianie. Takie postępowanie pozwala na utworzenie wzoru skróconego mnożenia, a następnie na jego „zwinięcie” co w wyrażeniach trygonometrycznych pozwala często na uzyskanie jedynki trygonometrycznej lub innego bardziej satysfakcjonującego wzoru.
Zajmiemy się lewą stroną, gdzie dopiszemy wyrażenie 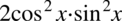 , a następnie je odejmiemy. Dlaczego akurat takie? Staramy się dążyć do wzoru skróconego mnożenia postaci
, a następnie je odejmiemy. Dlaczego akurat takie? Staramy się dążyć do wzoru skróconego mnożenia postaci 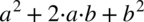 , naszymi „końcówkami”
, naszymi „końcówkami” 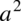 i
i 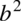 są odpowiednio
są odpowiednio 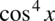 oraz
oraz 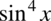 , poza tym wyrażenie te występuje po prawej stronie tożsamości. Być może wykładniki w postaci czwórek zamazują nieco obraz wzoru, ale możemy je przecież zapisać inaczej
, poza tym wyrażenie te występuje po prawej stronie tożsamości. Być może wykładniki w postaci czwórek zamazują nieco obraz wzoru, ale możemy je przecież zapisać inaczej 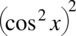 oraz
oraz 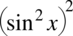 (co podniesione do kwadratu daje
(co podniesione do kwadratu daje 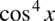 oraz
oraz 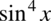 ). Do wzoru skróconego mnożenia potrzebujemy jeszcze „środka”
). Do wzoru skróconego mnożenia potrzebujemy jeszcze „środka” 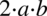 . Jeżeli odpowiedzieliśmy sobie na pytanie: co podniesione do kwadratu daje
. Jeżeli odpowiedzieliśmy sobie na pytanie: co podniesione do kwadratu daje 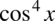 oraz
oraz 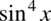 to mamy już
to mamy już 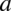 i
i 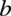 , które możemy podstawić do „środka” wzoru
, które możemy podstawić do „środka” wzoru 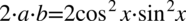 , dzięki czemu otrzymujemy pełny wzór skróconego mnożenia
, dzięki czemu otrzymujemy pełny wzór skróconego mnożenia 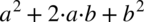 , który bez przeszkód zwinąć do postaci
, który bez przeszkód zwinąć do postaci 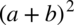 :
:
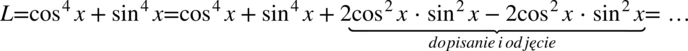
Teraz zamienię nieco kolejność aby utworzyć wzór skróconego mnożenia, ale wartość lewej strony nie ulegnie zmianie:
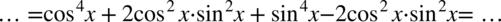
Nałożymy też nawias na potencjalny wzór, co również nie zmienia wartości wyrażenia:
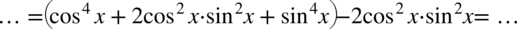
Jeszcze raz rozpisanie wzoru skróconego mnożenia:
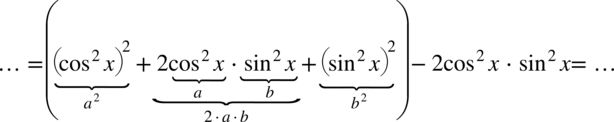
I jego zwinięcie do postaci 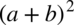 :
:
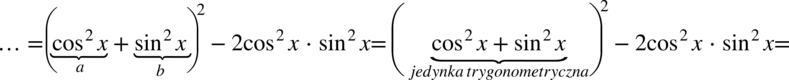
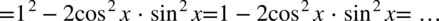
Na samym końcu zamienimy kolejność składników w wyrażeniu 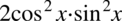 na
na 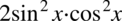 , ponieważ w wypadku mnożenia kolejność składników nie gra roli np.
, ponieważ w wypadku mnożenia kolejność składników nie gra roli np.  i nie zmienia ostatecznej wartości wyrażenia:
i nie zmienia ostatecznej wartości wyrażenia:
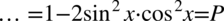

Przykład 75
[kliknij aby rozwinąć] 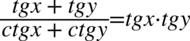
Założenie: 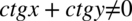 (mianownik nie może być równy
(mianownik nie może być równy  ). Po przekształceniu założenia otrzymujemy
). Po przekształceniu założenia otrzymujemy  .
.
Lewa strona tożsamości jest dłuższa, zatem to ona będzie przekształcana. Po prawej stronie do której dążymy występują wyłącznie tangensy, zatem wszelkie cotangensy znajdujące się po lewej stronie zlikwidujemy korzystając ze wzoru  oraz
oraz  . Nie ma potrzeby zamiany tangensów na sinusy i cosinusy, bo przykład niepotrzebnie się rozrośnie, ale oczywiście można tak postąpić:
. Nie ma potrzeby zamiany tangensów na sinusy i cosinusy, bo przykład niepotrzebnie się rozrośnie, ale oczywiście można tak postąpić:
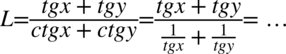
Powstałe po zamianie ze wzoru ułamki sprowadźmy do wspólnego mianownika:
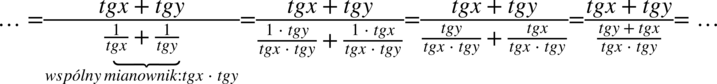
Teraz pozbędziemy się piętrowego ułamka zastępując główną kreskę ułamkową znakiem dzielenia, a następnie wymnażając przez odwrotność:
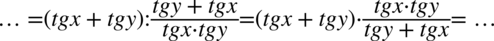
Dla ułatwienia działań zastosujemy zapis 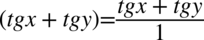 (kreska ułamkowa jest na tyle silna, że możemy pozbyć się nawisu):
(kreska ułamkowa jest na tyle silna, że możemy pozbyć się nawisu):
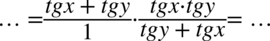
Po przekątnej mamy identyczne wyrażenia (kolejność w dodawaniu nie jest istotna), które można bez obaw skrócić:
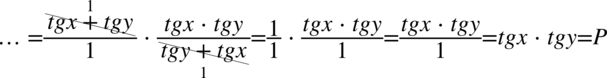

Przykład 76
[kliknij aby rozwinąć] 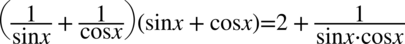
Założenie: 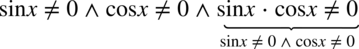 (żaden mianownik nie może być równy
(żaden mianownik nie może być równy  ). Iloczyn sinusa i cosinusa nie będzie równy zero gdy jednocześnie ani sinus ani cosinus nie będzie równy zeru. Ostatecznie otrzymujemy
). Iloczyn sinusa i cosinusa nie będzie równy zero gdy jednocześnie ani sinus ani cosinus nie będzie równy zeru. Ostatecznie otrzymujemy 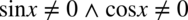 , aby się nie powtarzać.
, aby się nie powtarzać.
Lewa strona tożsamości jest zdecydowanie dłuższa, zatem to ona będzie przekształcana. Na początku pozbędziemy się nawiasów wymnażając kolejno składniki:
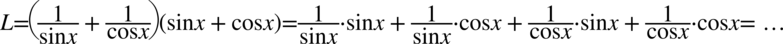
Aby rozwiać wątpliwości odnośnie mnożenia przez górę czy dół ułamka lub skracania zostanie zastosowany zapis 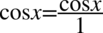 oraz
oraz 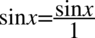 , ponieważ jakakolwiek liczba czy znak podzielony przez
, ponieważ jakakolwiek liczba czy znak podzielony przez  nie ulega zmianie:
nie ulega zmianie:
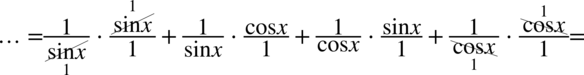
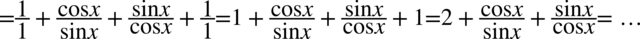
Na tym etapie powstała liczba i dwa ułamki. Dążąc do uzyskania prawej strony tożsamości należy stworzyć jedną kreskę ułamkową, a więc powstałe ułamki sprowadzimy do wspólnego mianownika: