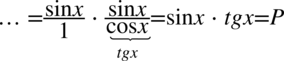Przykład 69
[kliknij aby rozwinąć] 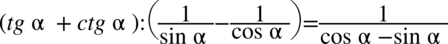
Założenie: 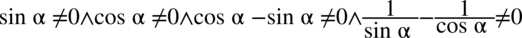 (żaden z mianowników nie może być równy
(żaden z mianowników nie może być równy  , ostatni warunek dotyczy tego, że nie można dzielić przez
, ostatni warunek dotyczy tego, że nie można dzielić przez  ). Po przekształceniach otrzymujemy
). Po przekształceniach otrzymujemy 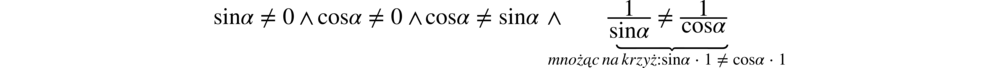 i ostatecznie:
i ostatecznie: 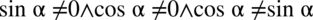 , aby nie powielać powtarzających się dwóch ostatnich rezultatów.
, aby nie powielać powtarzających się dwóch ostatnich rezultatów.
Lewa strona tożsamości jest dłuższa, zatem to ona będzie przekształcana. Między nawiasami występuje znak dzielenia, który można zastąpić kreską ułamkową. Na dalszych etapach z pewnością wrócimy do zapisu z  , ale na razie dzięki zapisowi z kreską ułamkową zapis będzie znacznie bardziej przejrzysty:
, ale na razie dzięki zapisowi z kreską ułamkową zapis będzie znacznie bardziej przejrzysty:
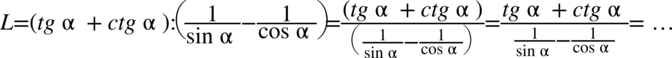
Nawiasy zostały usunięte, ponieważ kreska ułamkowa jest wystarczającą „granicą” oddzielającą wyrażenia.
Po prawej stronie do której dążymy nie występują ani tangensy ani cotangensy, zatem pozbędziemy się ich korzystając ze wzorów  oraz
oraz 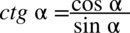 :
:
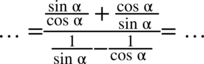
Teraz powstałe ułamki z licznika i mianownika ogromnego ułamka sprowadzimy do wspólnego mianownika:
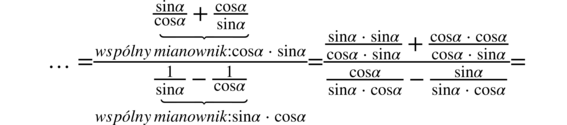
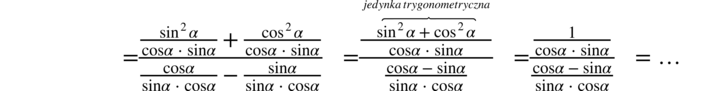
Teraz pozbędziemy się głównej kreski ułamkowej wracając do znaku dzielenia i zamienimy dzielenie na mnożenie odwracając drugi ułamek:


Skracanie było możliwe, ponieważ między skracanymi elementami występował znak mnożenia.
Przykład 70
[kliknij aby rozwinąć] 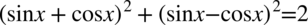 próbna matura 2010
próbna matura 2010
Lewa strona tożsamości jest wyraźnie dłuższa, zatem to ona będzie przekształcana. Na początku pozbędziemy się nawiasów korzystając ze wzorów skróconego mnożenia 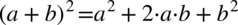 oraz
oraz 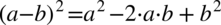 :
:
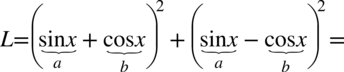
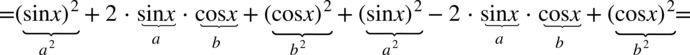
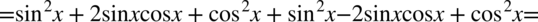


Przykład 71
[kliknij aby rozwinąć] 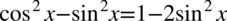
Obie strony tożsamości mają podobną długość. Poniżej zostaną zaprezentowane dwa sposoby udowodnienie równości.
I sposób
Zajmiemy się lewą stroną i będziemy ją przekształcać do prawej. Po prawej stronie, którą chcemy otrzymać występuje wyłącznie sinus, natomiast po lewej stronie sinus i cosinus, zatem pierwszym krokiem będzie zamiana cosinusa na sinus ze wzoru na przekształconą jedynkę trygonometryczną 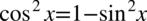 :
:
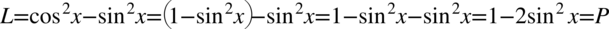

II sposób
Zaczniemy od prawej strony, występuje tu sinus i jedynka, a po lewej stronie do której uzyskania dążymy oprócz sinusa występuje także cosinus. Aby uzyskać cosinus rozbijemy jedynkę z godnie ze wzorem 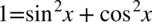 . W dłuższych przykładach starajmy się raczej zwijać do jedynki niż rozpisywać ją na sinus i cosinus, ponieważ już spory przykład może rozrosnąć się do ogromnych rozmiarów, natomiast w tym przypadku nie ma takiego niebezpieczeństwa:
. W dłuższych przykładach starajmy się raczej zwijać do jedynki niż rozpisywać ją na sinus i cosinus, ponieważ już spory przykład może rozrosnąć się do ogromnych rozmiarów, natomiast w tym przypadku nie ma takiego niebezpieczeństwa:
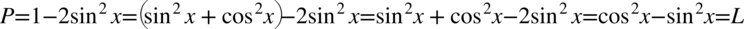

Przykład 72
[kliknij aby rozwinąć] 
Założenie: 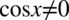 (mianownik nie może wynosić
(mianownik nie może wynosić  )
)
Obie strony tożsamości mają podobną długość, a jej udowodnienie można przeprowadzić na dwa sposoby.
I sposób
Zaczniemy od prawej strony, występuje tu tangens, a po lewej stronie nie. Także pierwszym krokiem będzie zamiana tangensa zgodnie ze wzorem 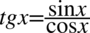 :
:

Dla ułatwienia dalszych działań zastosujemy zapis 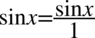 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez  nie ulega zmianie:
nie ulega zmianie:

Przyjrzyjmy się teraz lewej stronie do której dążymy, występują tu wyłącznie cosinusy. W liczniku powstałego ułamka mamy sinus podniesiony do kwadratu co pozwala na bezproblemową zamianę na cosinus ze wzoru na przekształconą jedynkę trygonometryczną 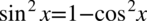 :
:

Na razie mamy jeden ułamek, a po lewej stronie oprócz jednej kreski ułamkowej występuje cosinus za ułamkiem, dlatego teraz rozdzielimy powstały ułamek na dwa tak jak się to wykonuje na prostszych liczbach np. 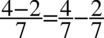 i wykonajmy skracanie:
i wykonajmy skracanie:
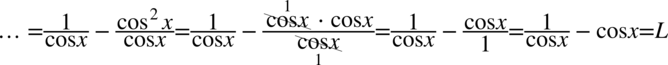

II sposób
Zaczniemy od lewej strony, pierwszym krokiem będzie wciągnięcie cosinusa stojącego za ułamkiem na kreskę ułamkową przez sprowadzenie do wspólnego mianownika. Dla ułatwienia działań zostanie użyty zapis 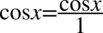 :
:
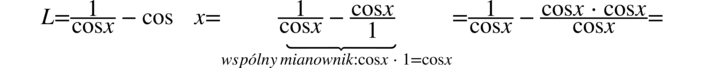

Aby uzyskać prawą stronę tożsamości musimy otrzymać tangens, który rozpisuje się ze wzoru 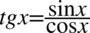 , dążąc do tego rozpiszemy sinus podniesiony do kwadratu na iloczyn dwóch sinusów:
, dążąc do tego rozpiszemy sinus podniesiony do kwadratu na iloczyn dwóch sinusów:

Teraz możemy rozdzielić mnożenie na dwie kreski ułamkowe i zapisać iloraz sinusa przez cosinus w postaci tangensa: