
Przykład 65
[kliknij aby rozwinąć] 
Założenie: 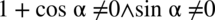 (żaden z mianowników nie może być równy
(żaden z mianowników nie może być równy  ). Po przekształceniu ostatecznie otrzymujemy
). Po przekształceniu ostatecznie otrzymujemy 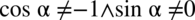 .
.
Lewa strona tożsamości jest dłuższa, zatem to ona będzie przekształcana. Pierwsza czynność będzie polegała na zlikwidowaniu cotangensa korzystając ze wzoru 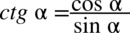 , ponieważ po lewej stronie do której dążymy cotangens nie występuje:
, ponieważ po lewej stronie do której dążymy cotangens nie występuje:
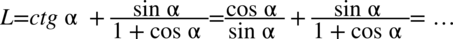
Powstały dwa ułamki, teraz stworzymy dla nich wspólny mianownik, ponieważ po prawej stronie występuje jeden ułamek:
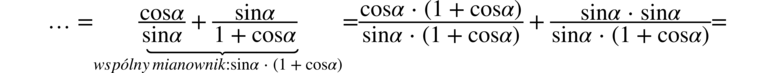
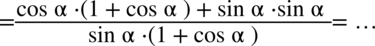
Teraz pozbędziemy się nawiasów w liczniku wymnażając kolejno składniki, natomiast z wymnażaniem mianownika warto się wstrzymać, ponieważ możemy w kolejnych etapach nie zauważyć możliwości skracania, a wymnożyć można zawsze później:
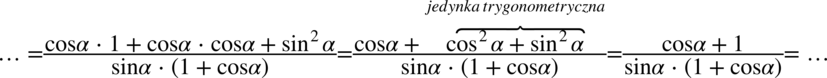
W liczniku powstało identyczne wyrażenie jak nawias w mianowniku, także można spokojnie skrócić obydwa wyrażenia:
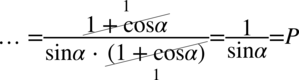

Przykład 66
[kliknij aby rozwinąć] 
Założenie: 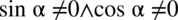 (żaden z mianowników nie może być równy
(żaden z mianowników nie może być równy  )
)
Od razu przestrzegam przed skracaniem w stylu 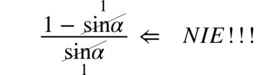 .Nie można tego wykonać, ponieważ pomiędzy składnikami w liczniku jest minus. Aby skracanie było wykonalne znak odejmowania wraz z otaczającymi go elementami musi być zamknięty w nawiasie:
.Nie można tego wykonać, ponieważ pomiędzy składnikami w liczniku jest minus. Aby skracanie było wykonalne znak odejmowania wraz z otaczającymi go elementami musi być zamknięty w nawiasie: 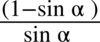 . Pojedynczych elementów z nawiasu nie wolno skracać i jak widać nie ma z czym skrócić sinusa z mianownika.
. Pojedynczych elementów z nawiasu nie wolno skracać i jak widać nie ma z czym skrócić sinusa z mianownika.
Podobnie ma się rzecz ze skracaniem 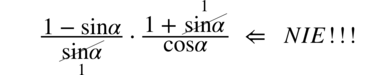 . W liczniku drugiego ułamka występuje dodawanie co uniemożliwia skracanie tak jak we wcześniejszym przypadku.
. W liczniku drugiego ułamka występuje dodawanie co uniemożliwia skracanie tak jak we wcześniejszym przypadku.
Lewa strona tożsamości jest dłuższa, zatem to ona będzie przekształcana. Pomiędzy ułamkami mamy mnożenie także można zapisać je na jednej kresce ułamkowej:
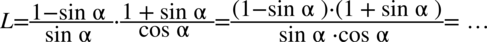
Teraz pozbędziemy się nawiasów w liczniku powstałego ułamka. Można to zrobić wymnażając kolejno składniki, ale warto zauważyć, że nawiasy różnią się tylko jednym znakiem, poza tym szczegółem są identyczne, dlatego można zastosować tu wzór skróconego mnożenia 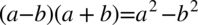 (efekt będzie taki sam):
(efekt będzie taki sam):
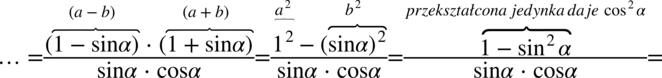
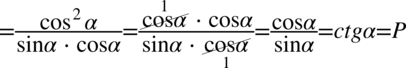

Na końcu zastosowano wzór  .
.
Przykład 67
[kliknij aby rozwinąć] 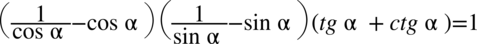
Założenie: 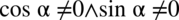 (żaden z mianowników nie może być równy
(żaden z mianowników nie może być równy  )
)
Lewa strona równania jest dłuższa, zatem to ona będzie przekształcana. Na początku pozbędziemy się nawiasów wymnażając kolejno składniki z pierwszych dwóch nawiasów. Wynik zapiszemy w nawiasie, ponieważ mamy w perspektywie wymnożenie kolejnego nawiasu:
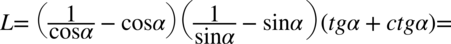
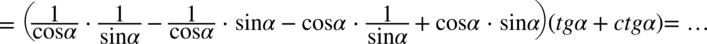
Teraz uprościmy zawartość pierwszego nawiasu, dla ułatwienia zostaną zastosowane zapisy 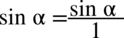 oraz
oraz 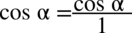 (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie):
nie ulega zmianie):
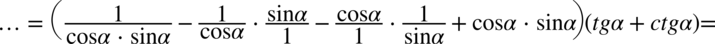
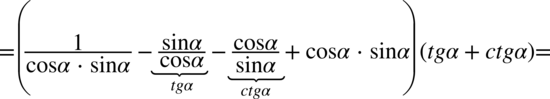
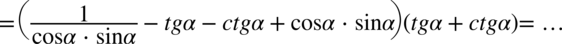
Kolejny etap stanowi wymnożenie dwóch nawiasów:
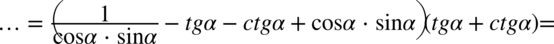
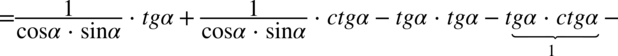
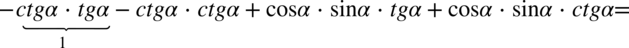
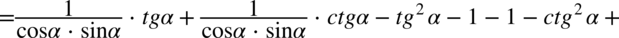
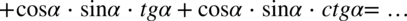
Teraz nie pozostaje nic innego niż pozbycie się tangensów i cotangensów ze wzorów  oraz
oraz 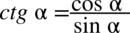 . Dla ułatwienia dalszych działań (skracania) zostanie zastosowany zapis
. Dla ułatwienia dalszych działań (skracania) zostanie zastosowany zapis 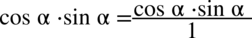 (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie):
nie ulega zmianie):

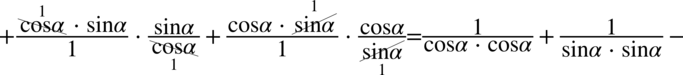
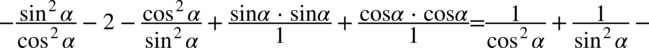
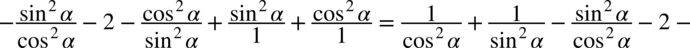
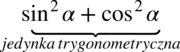
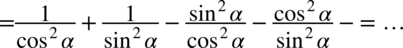
Aby w miarę sprawnie wykonać dalsze działania ułamki o tych samych mianownikach zapiszmy obok siebie. Pamiętajmy, że przy zmianie kolejności należy przenosić również znak występujący przed ułamkiem:
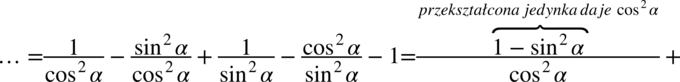
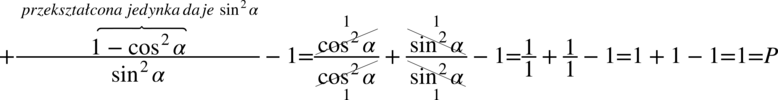

Przykład 68
[kliknij aby rozwinąć] 
Założenie:  (mianownik nie może być równy
(mianownik nie może być równy  ). Przekształcając założenie możemy wyciągnąć
). Przekształcając założenie możemy wyciągnąć  przed nawias co daje
przed nawias co daje 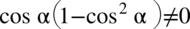 . Warto też rozpisać powstały nawias ze wzoru skróconego mnożenia
. Warto też rozpisać powstały nawias ze wzoru skróconego mnożenia 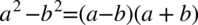 :
:


Otrzymujemy: 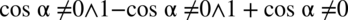 (każdy z czynników musi być różny od zera, ponieważ iloczyn trzech składników będzie równy od zera tylko wtedy, gdy każdy z nich będzie różny od zera – każda liczba wymnożona przez
(każdy z czynników musi być różny od zera, ponieważ iloczyn trzech składników będzie równy od zera tylko wtedy, gdy każdy z nich będzie różny od zera – każda liczba wymnożona przez  daje
daje  )
)
Wykonujemy ostatnie przekształcenia: 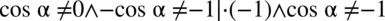 i ostatecznie otrzymujemy:
i ostatecznie otrzymujemy: 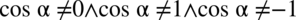 .
.
Lewa strona tożsamości jest zdecydowanie dłuższa, także to ona będzie przekształcana. Na pierwszy rzut oka nie można tu dostrzec podstawowych wzorów np. jedynki trygonometrycznej lub jej przekształceń. Przyjrzyjmy się mianownikowi ułamka – można tu wyciągnąć cosinus przed nawias:
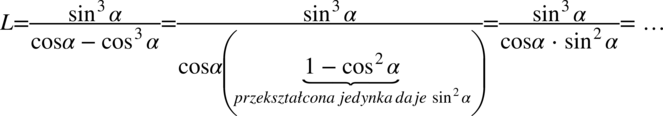
W liczniku i mianowniku ułamka występuje wyłącznie mnożenie, także można skracać bez obaw, dla wygody rozpiszemy licznik:
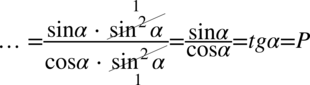

Na końcu otrzymaliśmy wzór 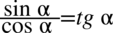 .
.