
Przykład 61
[kliknij aby rozwinąć] 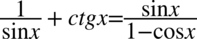
Założenie: 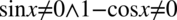 (żaden mianownik nie może być równy
(żaden mianownik nie może być równy  ). Przekształcając otrzymujemy
). Przekształcając otrzymujemy 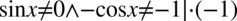 i ostatecznie
i ostatecznie 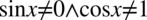 .
.
Po lewej stronie tożsamości występuje cotangens, co daje więcej możliwości, także to właśnie tą stronę będziemy przekształcać. Zaczniemy od zlikwidowania cotangensa korzystając ze wzoru 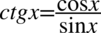 :
:
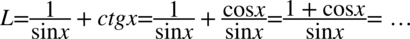
Teraz zapraszam to przeanalizowania przykładu 34, bo od tego etapu tożsamość wygląda identycznie.
Przykład 62
[kliknij aby rozwinąć] 
Będziemy przekształcać prawą stronę, ponieważ znajduje się tu nawias. Zaczynamy właśnie od wymnożenia tangensa przez składniki z nawiasu:
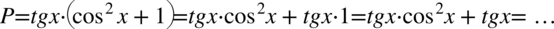
Patrząc na lewą stronę, którą mamy uzyskać, zlikwidujemy tangens znajdujący się przy cosinusie korzystając ze wzoru 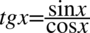 , drugi tangens zostawiamy w spokoju, ponieważ występuje po prawej stronie tożsamości:
, drugi tangens zostawiamy w spokoju, ponieważ występuje po prawej stronie tożsamości:
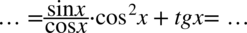
Dla ułatwienia rachunków zostanie zastosowany zapis 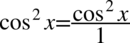 (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie):
nie ulega zmianie):
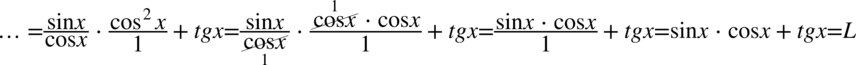

Przykład 63
[kliknij aby rozwinąć] 
W tym przykładzie obie strony mają podobną długość, jednak po lewej stronie występują wyższe wartości potęg i to właśnie lewa strona będzie przekształcana. Trzeba się tu wykazać znajomością wzorów skróconego mnożenia. Na początku zapiszemy czwórki z wykładników potęg za pomocą dwójek, ponieważ po prawej stronie znajdują się właśnie dwójki:
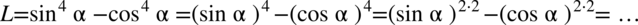
Teraz skorzystamy z własności potęg, gdzie  :
:
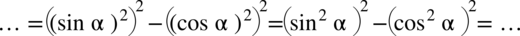
Teraz przyjrzyjmy się powstałemu wynikowi - mamy dwa elementy poniesione do kwadratu, które są oddzielone znakiem minus. I w tym momencie trzeba użyć wzoru skróconego mnożenia 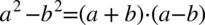 do rozłożenia powstałego wyrażenia na czynniki (czyli iloczyn nawiasów):
do rozłożenia powstałego wyrażenia na czynniki (czyli iloczyn nawiasów):
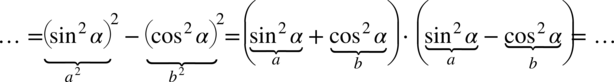
Teraz przyjrzyjmy się zawartości nawiasów, w pierwszym z nich otrzymaliśmy jedynkę trygonometryczną:
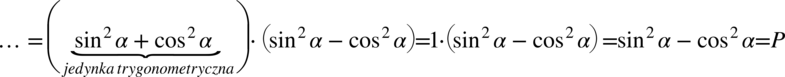

Przykład 64
[kliknij aby rozwinąć] 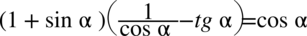
Założenie: 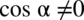 (mianownik w ułamku nie może być równy
(mianownik w ułamku nie może być równy  )
)
Lewa strona równości jest zdecydowanie dłuższa, zatem to ona będzie przekształcana. Na początku pozbędziemy się nawiasów wymnażając kolejno składniki:
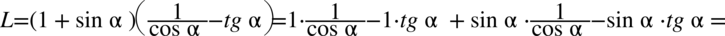
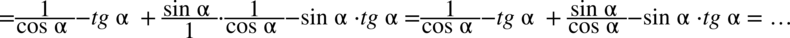
Dla ułatwienia rachunków zastosowano zapis 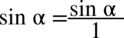 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez  nie ulega zmianie. Po wymnożeniu warto przyjrzeć się, czy nie otrzymaliśmy konkretnych wzorów i tu mamy
nie ulega zmianie. Po wymnożeniu warto przyjrzeć się, czy nie otrzymaliśmy konkretnych wzorów i tu mamy 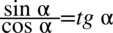 :
:
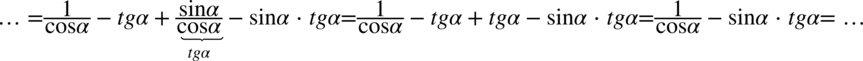
Teraz pozbędziemy się tangensa, ponieważ po prawej stronie do której dążymy tangens nie występuje. Korzystamy ze wzoru  :
:
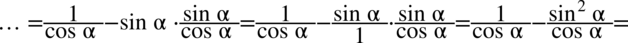
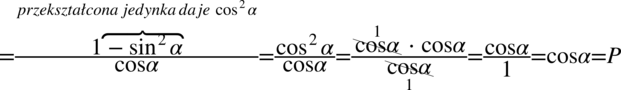

Dla ułatwienia rachunków ponownie zastosowano zapis 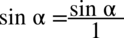 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez  nie ulega zmianie.
nie ulega zmianie.