Przykład 57
[kliknij aby rozwinąć] 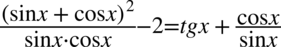
Założenie: 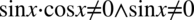 (żaden z mianowników nie może być równy
(żaden z mianowników nie może być równy  ). Otrzymujemy
). Otrzymujemy 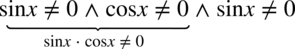 , ponieważ iloczyn dwóch liczb jest różny od zera, jeżeli każda z tych liczb osobno jest różna od zera. Ostatecznie mamy
, ponieważ iloczyn dwóch liczb jest różny od zera, jeżeli każda z tych liczb osobno jest różna od zera. Ostatecznie mamy 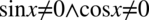 (aby nie powtarzać tego samego).
(aby nie powtarzać tego samego).
Od razu przestrzegam przed skracaniem w stylu
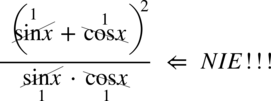 .
.
Dodawanie wraz z otaczającymi je elementami jest zamknięte w nawiasie, ale wnętrza nawiasu nie wolno ruszać! Dozwolone jest skracanie całego nawiasu z innym identycznym nawiasem.
Lewa strona równości jest dłuższa, zatem to ona będzie przekształcana. Na początku tradycyjnie pozbędziemy się nawiasów. W liczniku występuje wzór skróconego mnożenia w postaci 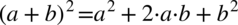 , po rozpisaniu otrzymujemy:
, po rozpisaniu otrzymujemy:
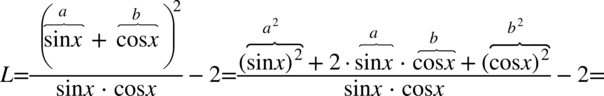

Znów ostrzegam przed skracaniem wyrażenia
 , ponieważ w liczniku jest dodawanie!
, ponieważ w liczniku jest dodawanie!
Teraz właściwie pozostaje wciągnięcie  znajdującej się poza ułamkiem na kreskę ułamkową poprzez sprowadzenie do wspólnego mianownika. Dla ułatwienia zostanie zastosowany zapis
znajdującej się poza ułamkiem na kreskę ułamkową poprzez sprowadzenie do wspólnego mianownika. Dla ułatwienia zostanie zastosowany zapis  (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie):
nie ulega zmianie):
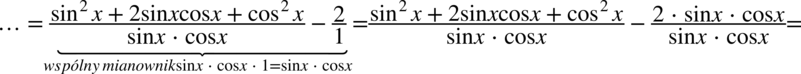

W liczniku pojawiła się jedynka trygonometryczna i oczywiście można zastosować zapis 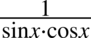 , ale przyjrzyjmy się prawej stronie tożsamości gdzie taka forma rozwiązania nie jest pożądany. W tym przypadku należy rozbić powstały ułamek na dwa oddzielne ułamki postępując zupełnie tak samo jak na prostych ułamkach
, ale przyjrzyjmy się prawej stronie tożsamości gdzie taka forma rozwiązania nie jest pożądany. W tym przypadku należy rozbić powstały ułamek na dwa oddzielne ułamki postępując zupełnie tak samo jak na prostych ułamkach 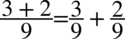 :
:

Skracanie było dozwolone, ponieważ w liczniku i mianowniku pomiędzy składnikami było wyłącznie mnożenie. Na koniec korzystamy ze wzoru 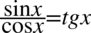 i ostatecznie otrzymujemy prawą stronę:
i ostatecznie otrzymujemy prawą stronę:


Przykład 58
[kliknij aby rozwinąć] 
Założenie: 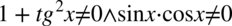 (żaden z mianowników nie może być równy
(żaden z mianowników nie może być równy  ). Otrzymujemy
). Otrzymujemy 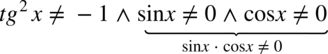 , ponieważ iloczyn dwóch liczb jest różny od zera, jeżeli każda z tych liczb osobno jest różna od zera, natomiast tangens podniesiony do kwadratu jest zawsze różny od
, ponieważ iloczyn dwóch liczb jest różny od zera, jeżeli każda z tych liczb osobno jest różna od zera, natomiast tangens podniesiony do kwadratu jest zawsze różny od  , bo jakakolwiek liczba podniesiona do kwadratu nigdy nie będzie ujemna. Także ostatecznie wystarczy zapisać
, bo jakakolwiek liczba podniesiona do kwadratu nigdy nie będzie ujemna. Także ostatecznie wystarczy zapisać 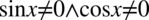 .
.
Tutaj także przestrzegam przed skracaniem w stylu
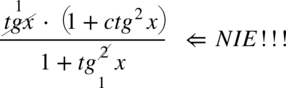 oraz
oraz
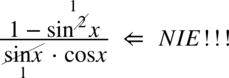 .
.
Aby było ono możliwe znak dodawania wraz z otaczającymi je elementami musi być zamknięty w nawiasie, a więc
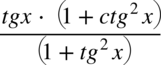 oraz
oraz
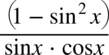 . Jak widać nie ma za bardzo z czym skracać, ponieważ elementów z wnętrza nawiasów nie wolno ruszać.
. Jak widać nie ma za bardzo z czym skracać, ponieważ elementów z wnętrza nawiasów nie wolno ruszać.
Lewa strona równości jest dłuższa, poza tym występują tu nawiasy oraz tangens i cotangens, które i tak trzeba będzie zamienić na sinusy i cosinusy, ponieważ po prawej stronie tożsamości znajdują się właśnie tylko one. Na początku tradycyjnie pozbędziemy się nawiasów wymnażając kolejno składniki:
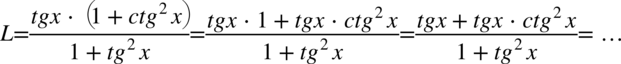
Rozpiszmy 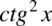 z licznika na
z licznika na 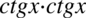 i skorzystamy ze wzoru
i skorzystamy ze wzoru 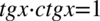 . Dzięki temu później będzie mniej rozpisywania, bo im więcej tangensów czy cotangensów tym więcej sinusów i cosinusów pojawiających się w wyniku rozpisania tych pierwszych:
. Dzięki temu później będzie mniej rozpisywania, bo im więcej tangensów czy cotangensów tym więcej sinusów i cosinusów pojawiających się w wyniku rozpisania tych pierwszych:
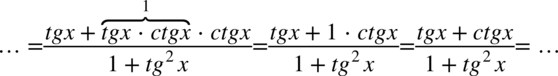
Kolejny etap to rozpisanie tangensa i cotangensa ze wzorów 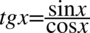 oraz
oraz 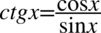 :
:
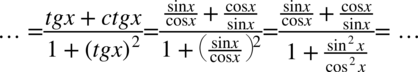
Teraz sprowadzimy do wspólnego mianownika ułamki powstałe w liczniku i w mianowniku, dla ułatwienia zostanie zastosowany zapis 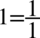 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez  nie ulega zmianie:
nie ulega zmianie:
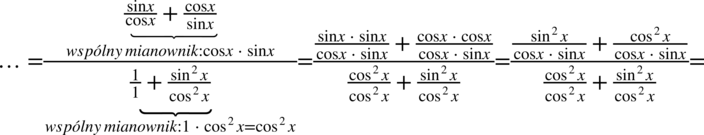
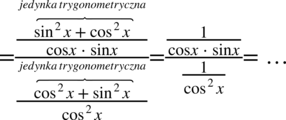
Teraz pozbędziemy się piętrowego ułamka zastępując główną kreskę ułamkową znakiem dzielenia i zamieniając dzielenie na mnożenie:
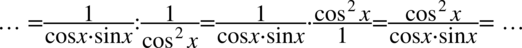
W ułamku występuje wyłącznie mnożenie pomiędzy składnikami w liczniku i mianowniku i właściwie można tu skracać, ale spójrzmy na prawą stronę tożsamości, która różni się tylko licznikiem od otrzymanego wyniku. Nie będziemy tu skracać cosinusa, ponieważ zniknie on wtedy z mianownika. Przyjrzyjmy się licznikowi ułamka, występuje tu cosinus podniesiony do kwadratu i można skorzystać ze wzoru na przekształcenie jedynki trygonometrycznej 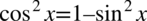 . Tym samym otrzymujemy żądaną prawą stronę:
. Tym samym otrzymujemy żądaną prawą stronę:


Przykład 59
[kliknij aby rozwinąć] 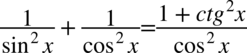
Założenie: 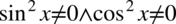 . Wynika z tego
. Wynika z tego 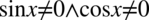 , ponieważ jeżeli sinus (cosinus) podniesiony do kwadratu jest różny od zera, to również sam sinus (cosinus) musi być różny od zera.
, ponieważ jeżeli sinus (cosinus) podniesiony do kwadratu jest różny od zera, to również sam sinus (cosinus) musi być różny od zera.
Zaczniemy przekształcanie od prawej strony, co prawda lewa strona wydaje się dłuższa, ale nie ma tam cotangensa, który łatwej jest rozpisać na sinus i cosinus niż zastawiać się jak z kilku sinusów i cosinusów stworzyć cotangens.
Przekształcanie tożsamości można wykonać na dwa sposoby. Pierwszy z nich zakłada rozdzielenie prawej strony na dwa ułamki, ponieważ po lewej stronie mamy właśnie dwie oddzielne kreski ułamkowe tak jak się to wykonuje na prostych liczbach 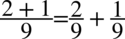 , później pozbędziemy się cotangensa korzystając ze wzoru
, później pozbędziemy się cotangensa korzystając ze wzoru 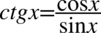 . Drugi sposób zakłada wykonanie tych samych czynności tylko w odwrotnej kolejności. Przeważanie ten pierwszy okazuje się krótszy, ale obydwa prowadzą do takiego samego rezultatu.
. Drugi sposób zakłada wykonanie tych samych czynności tylko w odwrotnej kolejności. Przeważanie ten pierwszy okazuje się krótszy, ale obydwa prowadzą do takiego samego rezultatu.
I sposób
Rozdzielmy prawą stronę na dwa ułamki, ponieważ po lewej stronie znajdują się dwie kreski ułamkowe analogicznie jak wykonuje się to na prostych liczbach 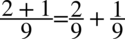 :
:
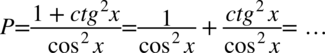
Teraz pozbędziemy się cotangensa korzystając ze wzoru 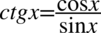 , ponieważ po lewej stronie występują same sinusy i cosinusy:
, ponieważ po lewej stronie występują same sinusy i cosinusy:
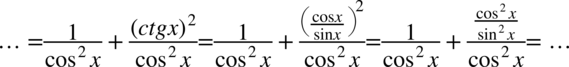
Teraz zlikwidujemy piętrowy ułamek zamieniając kreskę ułamkowa na znak dzielenia, a następnie mnożąc przez odwrotność, dla ułatwienia zostanie zastosowany zapis 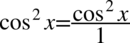 (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie):
nie ulega zmianie):
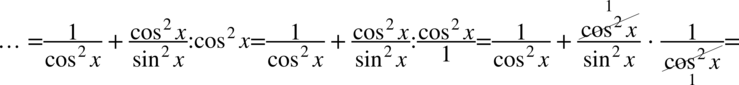
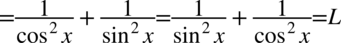

II sposób
Zaczniemy od rozpisania cotangensa występującego po prawej stronie ze wzoru 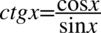 :
:
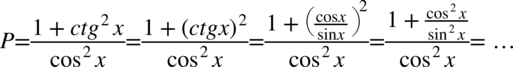
Teraz rozdzielimy duży ułamek na daw mniejsze ułamki znów stosując schemat
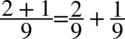 :
:
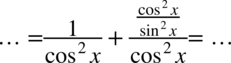
Teraz zlikwidujemy piętrowy ułamek zamieniając kreskę ułamkowa na znak dzielenia, a następnie mnożąc przez odwrotność, dla ułatwienia zostanie zastosowany zapis 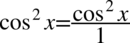 (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie):
nie ulega zmianie):
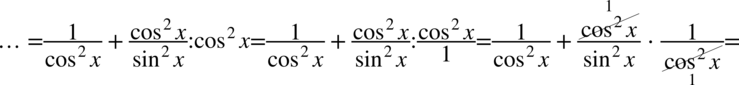
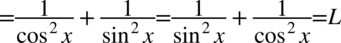

Przykład 60
[kliknij aby rozwinąć] 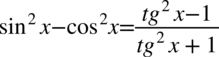
Założenie: 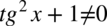 (mianownik nie może być równy
(mianownik nie może być równy  ). Po przekształceniu otrzymujemy
). Po przekształceniu otrzymujemy 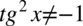 , przy czym zapis ten jest zawsze prawdą, ponieważ jakakolwiek liczba podniesiona do kwadratu jest różna od liczby ujemnej.
, przy czym zapis ten jest zawsze prawdą, ponieważ jakakolwiek liczba podniesiona do kwadratu jest różna od liczby ujemnej.
Znowu przestrzegam przed „kreatywnym” skracaniem typu  .Aby móc skracać odejmowanie lub dodawanie musi być zamknięte w nawiasie wraz z otaczającymi je elementami. Po zamknięciu dodawania / odejmowania w nawiasie nie ma już z czym skracać, ponieważ nie wolno ruszać wnętrza nawiasu:
.Aby móc skracać odejmowanie lub dodawanie musi być zamknięte w nawiasie wraz z otaczającymi je elementami. Po zamknięciu dodawania / odejmowania w nawiasie nie ma już z czym skracać, ponieważ nie wolno ruszać wnętrza nawiasu: 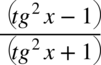 .
.
Będziemy przekształcać prawą stronę, która jest bardziej skomplikowana. Poza tym występują tu tangensy i zdecydowanie łatwiej zamienić je na sinusy i cosinusy niż postępować odwrotnie. Zaczniemy zatem od zlikwidowania tangensa korzystając ze wzoru 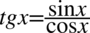 , ponieważ po lewej stronie tangens nie występuje:
, ponieważ po lewej stronie tangens nie występuje:
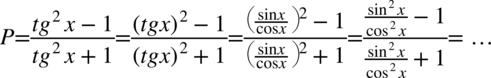
Teraz wciągniemy jedynki do nowo powstałych ułamków sprowadzając je do wspólnego mianownika, dla ułatwienia zostanie zastosowany zapis
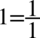 , ponieważ każda liczba podzielona przez
, ponieważ każda liczba podzielona przez
 nie ulega zmianie:
nie ulega zmianie:

Teraz zlikwidujemy piętrowy ułamek zamieniając główną kreską ułamkową na znak dzielenia, a następnie mnożąc przez odwrotność: