Przykład 53
[kliknij aby rozwinąć] 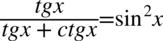
Założenie:  (mianownik nie może być równy
(mianownik nie może być równy  ). Po przekształceniu otrzymujemy
). Po przekształceniu otrzymujemy  .
.
Uprzedzam, że nie można stosować skracania typu 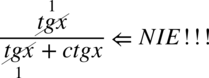 , ponieważ w mianowniku występuje dodawanie, a skracanie jest możliwe tylko wtedy, gdy dodawanie jest zamknięte w nawiasie wraz z otaczającymi je elementami
, ponieważ w mianowniku występuje dodawanie, a skracanie jest możliwe tylko wtedy, gdy dodawanie jest zamknięte w nawiasie wraz z otaczającymi je elementami 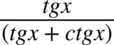 . Wnętrze nawiasu jest „święte” i nie można skracać stąd żadnego elementu, a poza nawiasem nie ma nic do skracania, (gdyby było to musi być znak mnożenia między tym elementem i nawiasem).
. Wnętrze nawiasu jest „święte” i nie można skracać stąd żadnego elementu, a poza nawiasem nie ma nic do skracania, (gdyby było to musi być znak mnożenia między tym elementem i nawiasem).
Lewa strona równości jest dłuższa, zatem to ją będziemy przekształcać, zaczniemy od skorzystania ze wzorów 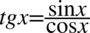 oraz
oraz 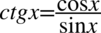 aby pozbyć się tangensa i cotangensa, ponieważ po prawej stronie występuje sinus.
aby pozbyć się tangensa i cotangensa, ponieważ po prawej stronie występuje sinus.

W mianowniku pierwotnego ułamka powstały dwa ułamki, które teraz sprowadzimy do wspólnego mianownika:

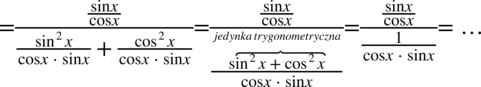
Teraz pozbędziemy się piętrowego ułamka zastępując główną kreskę ułamkową znakiem dzielenia i zamieniając dzielenie na mnożenie odwracając drugi ułamek i wykonać skracanie:
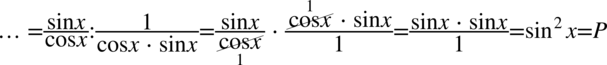

Przykład 54
[kliknij aby rozwinąć] 
Założenie:  (żaden mianownik nie może być równy
(żaden mianownik nie może być równy  ). Przekształcając założenie mamy
). Przekształcając założenie mamy 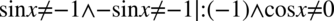 i ostatecznie otrzymujemy
i ostatecznie otrzymujemy 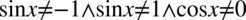 , ponieważ jeżeli cosinus podniesiony do kwadratu jest różny od zera, to tym bardziej sam cosinus jest różny od zera.
, ponieważ jeżeli cosinus podniesiony do kwadratu jest różny od zera, to tym bardziej sam cosinus jest różny od zera.
Uprzedzam, że nie wchodzi w grę skracanie w stylu 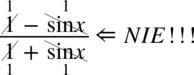 lub
lub 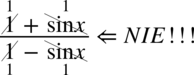 w żadnym z ułamków. Aby móc skracać odejmowanie lub dodawanie musi być zamknięte w nawiasie wraz z otaczającymi je elementami. Po zamknięciu dodawania / odejmowania w nawiasie nie ma już z czym skracać, ponieważ nie wolno ruszać wnętrza nawiasu:
w żadnym z ułamków. Aby móc skracać odejmowanie lub dodawanie musi być zamknięte w nawiasie wraz z otaczającymi je elementami. Po zamknięciu dodawania / odejmowania w nawiasie nie ma już z czym skracać, ponieważ nie wolno ruszać wnętrza nawiasu:  ,
,  .
.
Lewa strona równości jest dłuższa, zatem to ją będziemy przekształcać. Po lewej stronie mamy dwie kreski ułamkowe, a po prawej jedną, zatem pierwszym krokiem będzie sprowadzenie ułamków występujących po lewej stronie do wspólnego mianownika, zwłaszcza, że nie ma tu żadnych charakterystycznych wzorów np. przekształconej jedynki trygonometrycznej, a korzystanie z rozpisania 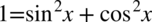 wykonujemy naprawdę w ostateczności:
wykonujemy naprawdę w ostateczności:
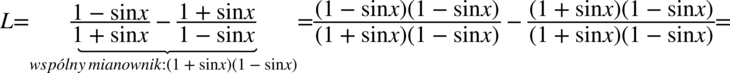

W liczniku powstałego ułamka zastosujemy wzory skróconego mnożenia 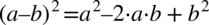 oraz
oraz 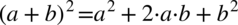 w celu jego uproszczenia. Rezultaty rozpisania wzorów zapiszemy jeszcze w nawiasach, ponieważ przed drugim nawiasem występuje minus, który spowoduje zmianę znaków w tymże nawiasie, o czym często się zapomina. Na razie zostawiamy mianownik w spokoju, ponieważ często się zdarza, że przedwczesne pozbycie się nawiasów może ukryć możliwość późniejszego skracania.
w celu jego uproszczenia. Rezultaty rozpisania wzorów zapiszemy jeszcze w nawiasach, ponieważ przed drugim nawiasem występuje minus, który spowoduje zmianę znaków w tymże nawiasie, o czym często się zapomina. Na razie zostawiamy mianownik w spokoju, ponieważ często się zdarza, że przedwczesne pozbycie się nawiasów może ukryć możliwość późniejszego skracania.
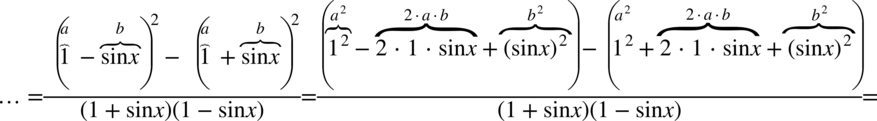

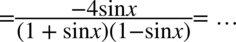
Właściwie licznik jest już zgodny z prawą stroną tożsamości, natomiast mianownik wymaga jeszcze przekształceń tzn. redukcji nawiasów, ponieważ nie ma tu żadnej możliwości skrócenia z licznikiem . Pozbędziemy się nawiasów korzystając ze wzoru skróconego mnożenia 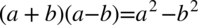 , ponieważ nawiasy są prawie identyczne, ale różnią się znakiem pośrodku. Oczywiście można nawiasy wymnożyć „na piechotę”, ale zastosowanie wzoru usprawnia liczenie.
, ponieważ nawiasy są prawie identyczne, ale różnią się znakiem pośrodku. Oczywiście można nawiasy wymnożyć „na piechotę”, ale zastosowanie wzoru usprawnia liczenie.
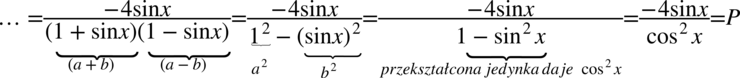

Przykład 55
[kliknij aby rozwinąć 
Założenie: 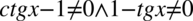 (żaden mianownik nie może być równy
(żaden mianownik nie może być równy  ), po przekształceniu mamy
), po przekształceniu mamy 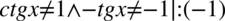 i ostatecznie otrzymujemy
i ostatecznie otrzymujemy  .
.
Od razu na wstępie przestrzegam przed błędnym skracaniem w stylu 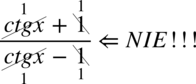 lub
lub 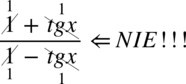 . Aby móc skracać odejmowanie lub dodawanie musi być zamknięte w nawiasie wraz z otaczającymi je elementami. Po zamknięciu dodawania / odejmowania w nawiasie nie ma już z czym skracać, ponieważ nie wolno ruszać wnętrza nawiasu:
. Aby móc skracać odejmowanie lub dodawanie musi być zamknięte w nawiasie wraz z otaczającymi je elementami. Po zamknięciu dodawania / odejmowania w nawiasie nie ma już z czym skracać, ponieważ nie wolno ruszać wnętrza nawiasu:  ,
, 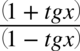 .
.
Obie strony równości są niemal identycznej długości. Powyższą tożsamość można udowodnić na kilka sposobów. Na początku zostaną zaprezentowane dwie krótsze metody, później dwie dłuższe. Nie ma sensu zamiana tangensów i cotangensów na sinusy i cosinusy (oczywiście jest to jak najbardziej dozwolone, ale to bardzo długi sposób), ponieważ występują właśnie tylko tangensy i cotangensy.
I sposób
Zaczniemy od lewej strony nietypowo wykorzystując rozpisanie jedynki w liczniku i mianowniku, ale ze wzoru 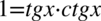 :
:
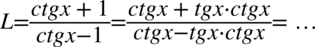
Teraz wyciągniemy przed nawias w liczniku i mianowniku 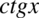 przed nawias. Należy pamiętać, że jeżeli „zabieramy” cały składnik przy wyciąganiu przed nawias, to zawsze zostaje tam
przed nawias. Należy pamiętać, że jeżeli „zabieramy” cały składnik przy wyciąganiu przed nawias, to zawsze zostaje tam  :
: 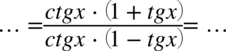
W tym momencie dodawanie i odejmowanie jest zamknięte w nawiasie, dlatego można już spokojnie skracać 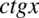 . Pamiętajmy, że elementów z wnętrza nawiasów nie wolno skracać, można skracać całe nawiasy jeśli są identyczne – tu akurat nie są identyczne.
. Pamiętajmy, że elementów z wnętrza nawiasów nie wolno skracać, można skracać całe nawiasy jeśli są identyczne – tu akurat nie są identyczne.
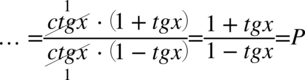

II sposób
Tym razem rozpiszemy prawą stronę równości korzystając z tego samego triku co w metodzie pierwszej, a więc rozpisania 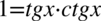 :
:
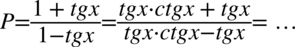
Teraz wyciągniemy przed nawias w liczniku i mianowniku 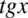 przed nawias. Należy pamiętać, że jeżeli „zabieramy” cały składnik przy wyciąganiu przed nawias, to zawsze zostaje tam
przed nawias. Należy pamiętać, że jeżeli „zabieramy” cały składnik przy wyciąganiu przed nawias, to zawsze zostaje tam  :
:
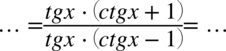
W tym momencie dodawanie i odejmowanie jest zamknięte w nawiasie, dlatego można już spokojnie skracać 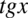 . Pamiętajmy, że elementów z wnętrza nawiasów nie wolno skracać, można skracać całe nawiasy jeśli są identyczne – tu akurat nie są identyczne.
. Pamiętajmy, że elementów z wnętrza nawiasów nie wolno skracać, można skracać całe nawiasy jeśli są identyczne – tu akurat nie są identyczne.
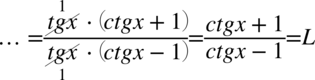

III sposób
Będziemy przekształcać lewą stronę, występują tu cotangensy, a po prawej stronie tangensy. Wobec tego skorzystamy ze wzoru  aby uzyskać wyłącznie tangensy:
aby uzyskać wyłącznie tangensy:
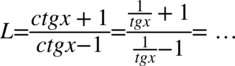
Teraz w liczniku i mianowniku należy wciągnąć  do nowo powstałych ułamków, sprowadzając je do wspólnego mianownika. Dla ułatwienia działań zostanie zastosowany zapis
do nowo powstałych ułamków, sprowadzając je do wspólnego mianownika. Dla ułatwienia działań zostanie zastosowany zapis 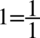 (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie):
nie ulega zmianie):
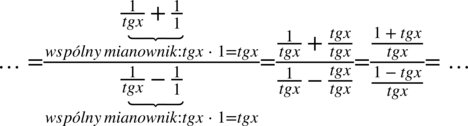
W tym momencie pozbędziemy się piętrowego ułamka zastępując główną kreskę ułamkową znakiem dzielenia i następnie zamienimy je na mnożenie odwracając drugi ułamek:
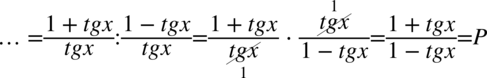

IV sposób
Będziemy przekształcać prawą stronę, występują tu tangensy, a po prawej stronie cotangensy. Wobec tego skorzystamy ze wzoru  aby uzyskać po tej stronie wyłącznie cotangensy:
aby uzyskać po tej stronie wyłącznie cotangensy:
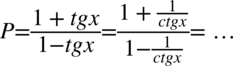
Teraz w liczniku i mianowniku należy wciągnąć  do nowo powstałych ułamków, sprowadzając je do wspólnego mianownika. Dla ułatwienia działań zostanie zastosowany zapis
do nowo powstałych ułamków, sprowadzając je do wspólnego mianownika. Dla ułatwienia działań zostanie zastosowany zapis 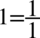 (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie):
nie ulega zmianie):
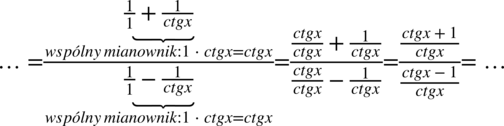
Na tym etapie pozbędziemy się piętrowego ułamka zastępując główną kreskę ułamkową znakiem dzielenia i następnie zamienimy je na mnożenie odwracając drugi ułamek:
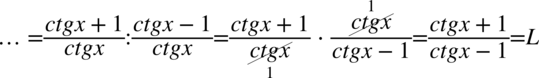

Przykład 52
[kliknij aby rozwinąć] 
Założenie: 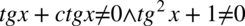 (żaden mianownik nie może być równy
(żaden mianownik nie może być równy  ). Po przekształceniu otrzymujemy
). Po przekształceniu otrzymujemy 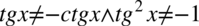 , przy czym drugi zapis jest zawsze prawdą, ponieważ jakakolwiek liczba podniesiona do kwadratu jest różna od liczby ujemnej.
, przy czym drugi zapis jest zawsze prawdą, ponieważ jakakolwiek liczba podniesiona do kwadratu jest różna od liczby ujemnej.
Znowu przestrzegam przed „kreatywnym” skracaniem typu 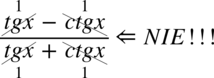 oraz
oraz 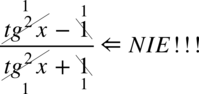 .Aby móc skracać odejmowanie lub dodawanie musi być zamknięte w nawiasie wraz z otaczającymi je elementami. Po zamknięciu dodawania / odejmowania w nawiasie nie ma już z czym skracać, ponieważ nie wolno ruszać wnętrza nawiasu:
.Aby móc skracać odejmowanie lub dodawanie musi być zamknięte w nawiasie wraz z otaczającymi je elementami. Po zamknięciu dodawania / odejmowania w nawiasie nie ma już z czym skracać, ponieważ nie wolno ruszać wnętrza nawiasu: 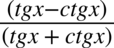 ,
, 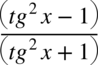 .
.
Obie strony równości mają podobną długość i właściwie daną tożsamość można udowodnić na dwa sposoby. Zamiana tangensów i cotangensów na sinusy i cosinusy jest oczywiście prawidłowa, ale nie ma to większego sensu, gdyż bardzo skomplikuje przekształcenia, poza tym nie ma tu funkcji sinus i cosinus.
I sposób
Zaczniemy od prawej strony nietypowo wykorzystując rozpisanie jedynki w liczniku i mianowniku, ale ze wzoru 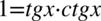 :
:
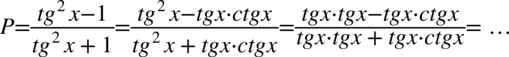
Teraz wyciągniemy przed nawias w liczniku i mianowniku 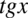 przed nawias:
przed nawias:
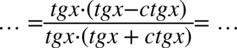
W tym momencie dodawanie i odejmowanie jest zamknięte w nawiasie, dlatego można już spokojnie skracać 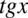 . Pamiętajmy, że elementów z wnętrza nawiasów nie wolno skracać, można skracać całe nawiasy jeśli są identyczne – tu akurat nie są identyczne.
. Pamiętajmy, że elementów z wnętrza nawiasów nie wolno skracać, można skracać całe nawiasy jeśli są identyczne – tu akurat nie są identyczne.
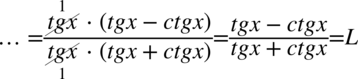

II sposób
Będziemy przekształcać lewą stronę równości zamieniając wszelkie cotangensy na tangensy korzystając ze wzoru  , ponieważ po prawej stronie nie ma cotangensów:
, ponieważ po prawej stronie nie ma cotangensów:
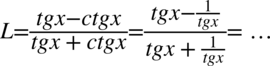
Teraz w liczniku i mianowniku należy wciągnąć 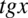 do nowo powstałych ułamków, sprowadzając je do wspólnego mianownika. Dla ułatwienia działań zostanie zastosowany zapis
do nowo powstałych ułamków, sprowadzając je do wspólnego mianownika. Dla ułatwienia działań zostanie zastosowany zapis 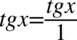 (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie):
nie ulega zmianie):
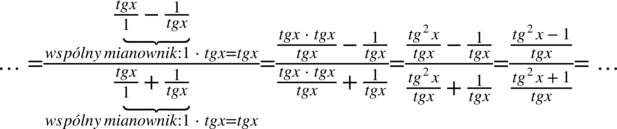
Na tym etapie pozbędziemy się piętrowego ułamka zastępując główną kreskę ułamkową znakiem dzielenia i następnie zamienimy je na mnożenie odwracając drugi ułamek: