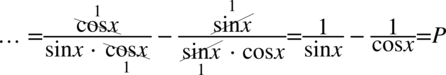Przykład 49
[kliknij aby rozwinąć] 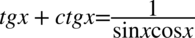
Założenie: 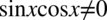 Otrzymujemy
Otrzymujemy  , ponieważ iloczyn dwóch liczb jest różny od
, ponieważ iloczyn dwóch liczb jest różny od  , jeżeli każda z liczb jest różna od
, jeżeli każda z liczb jest różna od  .
.
Na początku z lewej strony pozbędziemy się tangensa i cotangensa korzystając ze wzorów 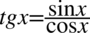 oraz
oraz 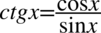 , ponieważ po prawej stronie nie występują:
, ponieważ po prawej stronie nie występują:

Po prawej stronie znajduje się jedna kreska ułamkowa, także dążąc do jej uzyskania sprowadzimy do wspólnego mianownika powstałe dwa ułamki:
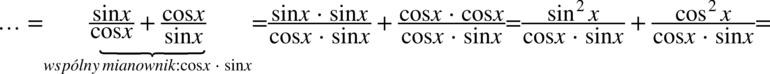
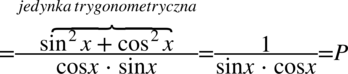

Przykład 50
[kliknij aby rozwinąć] 
Założenie: 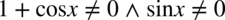 (żaden mianownik nie może być równy
(żaden mianownik nie może być równy  ). Ostatecznie otrzymujemy
). Ostatecznie otrzymujemy 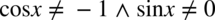 .
.
Obie strony równości mają podobną długość, w dodatku nie wiadomo od czego zacząć. Oczywiście można rozpisać  na sinus i cosinus korzystając z jedynki trygonometrycznej, ale na dłuższą metę nic to nie da, a przykład może się nam niepotrzebnie rozrosnąć. W tym przypadku trzeba użyć triku z domnażaniem.
na sinus i cosinus korzystając z jedynki trygonometrycznej, ale na dłuższą metę nic to nie da, a przykład może się nam niepotrzebnie rozrosnąć. W tym przypadku trzeba użyć triku z domnażaniem.
I sposób
Zaczniemy od lewej strony domnażając licznik i mianownik przez 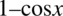 korzystając tym samym ze wzoru skróconego mnożenia
korzystając tym samym ze wzoru skróconego mnożenia 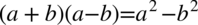 . Pamiętajmy, że przy domnażaniu mianownika nie można zapomnieć o liczniku, musi być sprawiedliwie :).
. Pamiętajmy, że przy domnażaniu mianownika nie można zapomnieć o liczniku, musi być sprawiedliwie :).
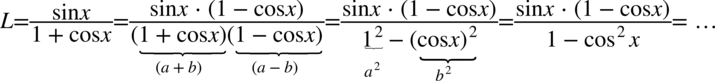
W jakim celu było nam to potrzebne? Otóż dzięki domnożeniu otrzymaliśmy w mianowniku przekształcenie jedynki trygonometrycznej 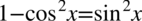 . Licznik celowo nie został wymnożony, aby „nie zakryć” możliwości skracania:
. Licznik celowo nie został wymnożony, aby „nie zakryć” możliwości skracania:
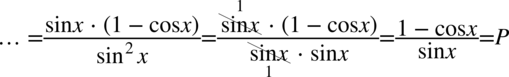

Tym razem skracanie jest dozwolone, ponieważ odejmowanie było zamknięte w nawiasie wraz z okalającymi je składnikami.
II sposób
Będziemy przekształcać prawą stronę pomnażając mianownik, a co za tym idzie i licznik przez 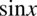 :
:

Celowo nie wymnażamy licznika, aby nie stracić z oczu możliwości skracania ułamka. Domnożenie pozwoliło uzyskać w mianowniku przekształconą jedynkę trygonometryczną 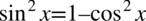 :
:

Teraz rozpiszemy mianownik korzystając ze wzoru skróconego mnożenia  :
:

Teraz już można spokojnie skracać, ponieważ dodawanie i odejmowanie jest zamknięte w nawiasach, a pomiędzy nawiasami jest znak mnożenia:
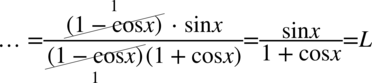

Przykład 51
[kliknij aby rozwinąć 
Założenie: 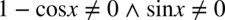 (żaden mianownik nie może być równy
(żaden mianownik nie może być równy  ). Przekształcając założenie mamy
). Przekształcając założenie mamy 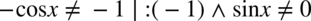 i ostatecznie otrzymujemy
i ostatecznie otrzymujemy  .
.
Lewa strona równości jest dłuższa, zatem tą ją będziemy przekształcać. Nie widać tu możliwości zastosowania charakterystycznych wzorów trygonometrycznych, ale po lewej stronie występują dwie kreski ułamkowe, także dążąc do uzyskania prawej strony należy stworzyć jedną kreskę ułamkową doprowadzając ułamki do wspólnego mianownika.
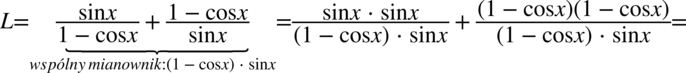

W liczniku drugiego ułamka pozbędziemy się nawiasów korzystając ze wzoru skróconego mnożenia 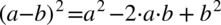 . Mianownika celowo nie wymnażamy aby nie stracić z oczu ewentualnego skracania.
. Mianownika celowo nie wymnażamy aby nie stracić z oczu ewentualnego skracania.
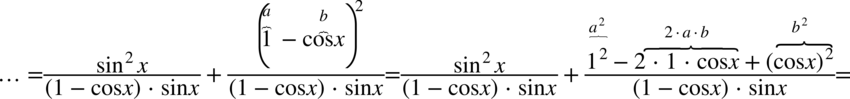

Zmieńmy kolejność składników w liczniku tak aby „przytulić” 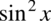 oraz
oraz 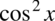 tak aby uzyskać jedynkę trygonometryczną:
tak aby uzyskać jedynkę trygonometryczną:
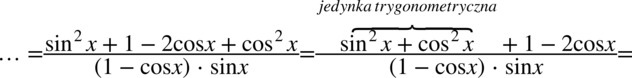
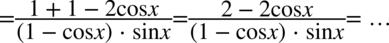
Wyciągnijmy przez nawias dwójkę z licznika, dzięki temu będzie możliwe skrócenie nawiasów z licznika i mianownika (dodawanie jest zamknięte w nawiasie):
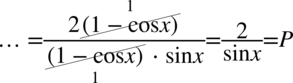

Przykład 52
[kliknij aby rozwinąć] 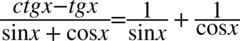
Założenie: 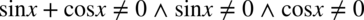 (żaden mianownik nie może być równy
(żaden mianownik nie może być równy  ). Ostatecznie otrzymujemy
). Ostatecznie otrzymujemy  .
.
Lewa strona równości daje większe możliwości przekształcenia. Na początku pozbędziemy się tangensa i cotangensa korzystając ze wzorów 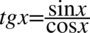 oraz
oraz 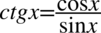 :
:
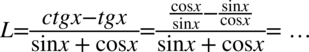
Teraz powstałe ułamki sprowadzimy do wspólnego mianownika:
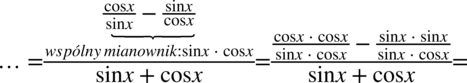
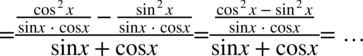
Warto na tym etapie pozbyć się piętrowego ułamka zastępując główną kreskę ułamkową znakiem dzielenia i wykonać dalsze działania tak jak na zwyczajnych ułamkach (zamieniając dzielenie na mnożenie):

Dla ułatwienia działań na ułamkach zastosowany zostanie zapis 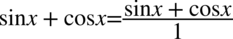 :
:

Na razie nie widać możliwości skracania, ale warto przyjrzeć się bliżej licznikowi pierwszego z ułamków. Występuje tu wzór skróconego mnożenia w postaci  , który można rozpisać
, który można rozpisać 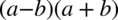 :
:
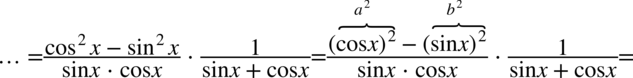
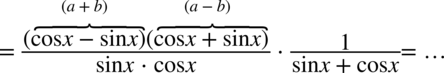
W tym momencie można już skracać na krzyż, ponieważ wszelkie dodawanie jest zamknięte w nawiasie:

Po prawej stronie do której dążymy występują dwie kreski ułamkowe, także powstały wynik rozdzielimy na dwa tak jak się to wykonuje na zwyczajnych ułamkach np. 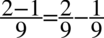 i można już skracać bez obaw, gdyż w obrębie każdego z ułamków występuje wyłącznie mnożenie:
i można już skracać bez obaw, gdyż w obrębie każdego z ułamków występuje wyłącznie mnożenie: