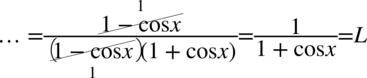Przykład 45
[kliknij aby rozwinąć] 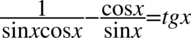
Założenie:  (żaden mianownik nie może być równy
(żaden mianownik nie może być równy  ). Otrzymujemy
). Otrzymujemy  z
z 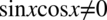 , ponieważ iloczyn dwóch liczb jest różny od
, ponieważ iloczyn dwóch liczb jest różny od  , jeżeli każda z liczb jest różna od
, jeżeli każda z liczb jest różna od  . Także ostatecznie mamy
. Także ostatecznie mamy  (nie ma sensu pisać powtarzających się elementów).
(nie ma sensu pisać powtarzających się elementów).
Lewa strona równości jest dłuższa, zatem to ją będziemy przekształcać. Na początku sprowadźmy wyrażenia do wspólnego mianownika, ponieważ na tym etapie przykład nie charakteryzuje się niczym szczególnym np. nie ma przekształconej jedynki trygonometrycznej.
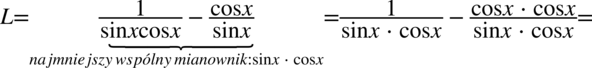
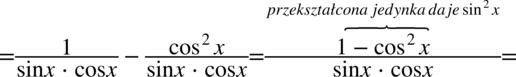


Przykład 46
[kliknij aby rozwinąć] 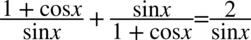
Założenie: 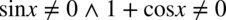 (żaden z mianowników nie może być równy
(żaden z mianowników nie może być równy  ). Po przekształceniu ostatecznie otrzymujemy
). Po przekształceniu ostatecznie otrzymujemy 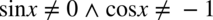 .
.
Lewa strona równości jest dłuższa, zatem to ją będziemy przekształcać. Po tej stronie występują dwa ułamki, a po prawej stronie jeden ułamek, także pierwszym krokiem będzie sprowadzenie tych ułamków do wspólnego mianownika, ponieważ na razie nie widać możliwości innych przekształceń.

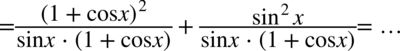
W pierwszym z ułamków skorzystamy przy pozbywaniu się nawiasu ze wzoru skróconego mnożenia 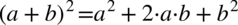 . Nie będziemy na razie wymnażać mianowników, ponieważ później możemy nie zauważyć ewentualnego skracania.
. Nie będziemy na razie wymnażać mianowników, ponieważ później możemy nie zauważyć ewentualnego skracania.
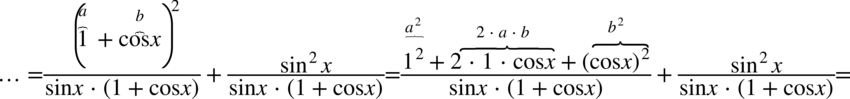
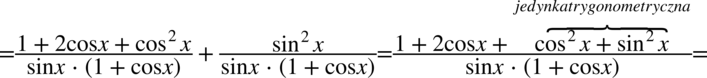
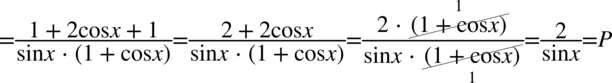

Przykład 47
[kliknij aby rozwinąć] 
Założenie: 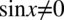 (mianownik nie może być równy
(mianownik nie może być równy  )
)
Lewa strona równości jest dłuższa, zatem to ją będziemy przekształcać. Na początku pozbędziemy się nawiasów wymnażając kolejno składniki.
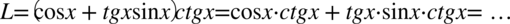
W drugim wyrażeniu zmieńmy nieco kolejność:
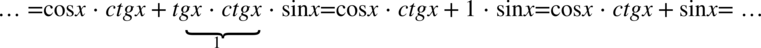
Teraz pozbędziemy się cotangensa korzystając ze wzoru 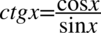 , ponieważ po lewej stronie nie występuje:
, ponieważ po lewej stronie nie występuje:
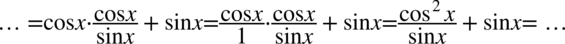
Aby było wiadomo w jaki sposób wymnożyć  zastosowano zapis
zastosowano zapis  (każda liczba podzielona przez
(każda liczba podzielona przez  nie ulega zmianie). Teraz wciągniemy
nie ulega zmianie). Teraz wciągniemy 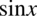 na kreskę ułamkową, ponieważ po prawej stronie do której otrzymania dążymy występuje ułamek bez innych składników. Dla ułatwienia znów zastosujemy zapis
na kreskę ułamkową, ponieważ po prawej stronie do której otrzymania dążymy występuje ułamek bez innych składników. Dla ułatwienia znów zastosujemy zapis 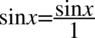 :
:
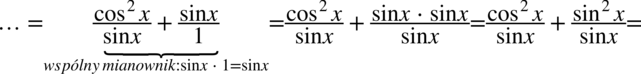
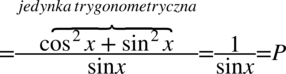

Przykład 48
[kliknij aby rozwinąć] 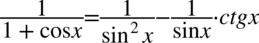
Założenie: 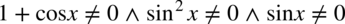 . Po przekształceniu otrzymujemy
. Po przekształceniu otrzymujemy 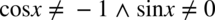 , ponieważ jeżeli sinus będzie różny od zera, to również sinus podniesiony do kwadratu również też będzie różny od zera.
, ponieważ jeżeli sinus będzie różny od zera, to również sinus podniesiony do kwadratu również też będzie różny od zera.
Od razu uprzedzam nie ma skracania w wyrażeniu 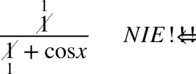 , ponieważ w mianowniku występuje dodawanie, a skracanie jest możliwe tylko wtedy, gdy dodawanie jest zamknięte w nawiasie wraz z otaczającymi je elementami
, ponieważ w mianowniku występuje dodawanie, a skracanie jest możliwe tylko wtedy, gdy dodawanie jest zamknięte w nawiasie wraz z otaczającymi je elementami 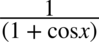 . Wnętrze nawiasu jest „święte” i nie można skracać stąd żadnego elementu, a poza nawiasem nie ma nic do skracania, (gdyby było to musi być znak mnożenia między tym elementem i nawiasem).
. Wnętrze nawiasu jest „święte” i nie można skracać stąd żadnego elementu, a poza nawiasem nie ma nic do skracania, (gdyby było to musi być znak mnożenia między tym elementem i nawiasem).
Tym razem prawa strona równania jest dłuższa, zatem to ją będziemy przekształcać. Na początku pozbędziemy się cotangensa korzystając ze wzoru 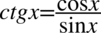 :
:
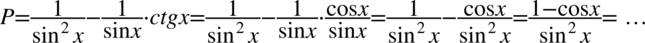
Teraz należy rozpisać mianownik powstałego ułamka korzystając z przekształconej jedynki trygonometrycznej 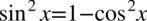 :
:
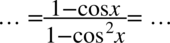
Zauważmy, że na dole mamy wzór skróconego mnożenia  , który rozpiszemy jako
, który rozpiszemy jako 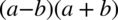 :
:
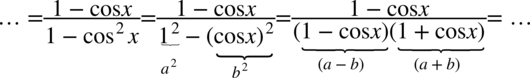
Teraz możemy już spokojnie skrócić cały mianownik z nawiasem z mianownika, ponieważ dodawanie zamknięte jest w nawiasie.